【仕事関連】quantmodで経済データを収集

やることはタイトルの通りです。どうやら、quantmodのgetSymbolsはFREDのデータも取れるらしく、株だけでなく経済データも取得できそうなので、それをやってみます。

library(quantmod)

symbols.name <- c("US Fixed Income","International Fixed Income","Emerging Fixed Income",
                  "US Equities","Europe Equities","Emerging Equities","US Real Estate",
                  "Ex-US Real Estate")
symbols <- c("BND","BNDX","VWOB","VTI","VGK","VWO","VNQ","VNQI")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE)
dats <- merge(BND,BNDX,VWOB,VTI,VGK,VWO,VNQ,VNQI)
dats <- Cl(dats)
colnames(dats) <- symbols.name
r_dats <- na.omit( ROC(dats, type = 'discrete') )
rm(BND,BNDX,VWOB,VTI,VGK,VWO,VNQ,VNQI,dats)

library(PerformanceAnalytics)
PerformanceAnalytics::charts.PerformanceSummary(r_dats)

# Yield Curve
symbols <- c("DTB3", "DGS2", "DGS5", "DGS10")
getSymbols(symbols, from = '1980-01-01', src = "FRED", auto.assign = TRUE)
spread_10y_2y <- DGS10 - DGS2
spread_2y_3m <- DGS2 - DTB3 
rm(DTB3, DGS2, DGS5)

# USD/YEN
getSymbols("DEXJPUS",from = '1980-01-01',src = "FRED")

symbols <- c("^GSPC","^DJI","^RUT")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE)
USequity <- Cl(merge(GSPC,DJI,RUT))
rm(DJI,RUT)
SPDJ_ratio <- USequity$GSPC.Close/USequity$DJI.Close
SPRS_ratio <- USequity$GSPC.Close/USequity$RUT.Close

symbols <- c("GDPC1","GOLDPMGBD228NLBM","POILBREUSDM","PCOPPUSDM","CPIAUCSL","PAYEMS")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE,src = "FRED")
CG_ratio <- PCOPPUSDM/GOLDPMGBD228NLBM

macro_indicator <- merge(GDPC1,CPIAUCSL,PAYEMS,DEXJPUS,GOLDPMGBD228NLBM,
                         PCOPPUSDM,POILBREUSDM,GSPC,DGS10,SPDJ_ratio,
                         SPRS_ratio,CG_ratio,spread_10y_2y,spread_2y_3m)
rm(CG_ratio,CPIAUCSL,DEXJPUS,DGS10,GDPC1,GOLDPMGBD228NLBM,PAYEMS,PCOPPUSDM,
   POILBREUSDM,GSPC,SPDJ_ratio,spread_10y_2y,spread_2y_3m,SPRS_ratio,USequity)

便利ですねー。

【仕事関連】Asset Allocation ModelをRで組んでみた。

おはこんばんにちは。勤め先で、アセットアロケーションに関するワークショップに参加したので、この分野は完全なる専門外ですがシミュレーションをしてみたいと思います。今回は、最小分散ポートフォリオ(minimum variance portfolio)を基本ポートフォリオとしたうえで、その分散共分散行列（予測値）をどのように推計するのかという点について先行研究を参考にエクササイズしていきたいと思います。先行研究は以下の論文です（オペレーションリサーチのジャーナルでした）。

papers.ssrn.com

最小分散ポートフォリオ

最小分散ポートフォリオの詳しい説明はここでは割愛しますが、要は各資産（内株、外株、内債、外債、オルタナ）のリターンの平均と分散を計算し、それらを縦軸平均値、横軸分散の二次平面にプロットしたうえで、投資可能範囲を計算し、その集合の中で最も分散が小さくなるポートフォリオの事らしいです（下図参照）。
f:id:osashimix:20190217131412p:plain
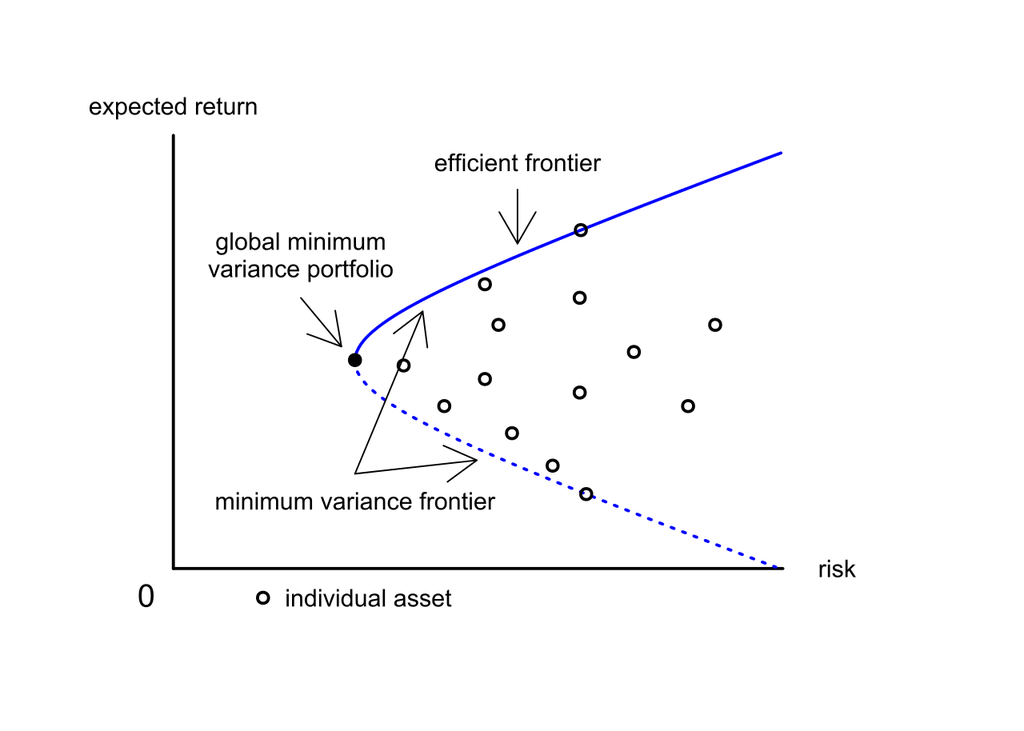
先行研究のCarroll et. al. (2017)では、「 this paper focusses on minimum-variance portfolios requiring only estimates of asset covariance, hence bypassing the well-known problem of estimation error in forecasting expected asset returns. 」と記載されており、現状でも期待リターンの推計は難しく、それを必要としない最小分散ポートフォリオは有益で実践的な手法であるといえます。最小分散ポートフォリオの目的関数は、その名の通り「分散を最小化すること」です。今、各資産のリターンを集めたベクトルをr、各資産の保有ウェイトを\theta、ポートフォリオリターンをR_{p}で表すことにすると、ポートフォリオ全体の分散var(R_{p})は以下のように記述できます。

var(R_{p}) = var(r^{T}\theta) = E( (r^{T}\theta)(r^{T}\theta)^{T}) = \theta^{T}\Sigma\theta

ここで\Sigmaはrの分散共分散行列です。よって、最小化問題は以下になります。

\min_{\theta}(\theta^{T}\Sigma\theta) \\ s.t 1^{T}\theta = 1

ここでは、フルインベストメントを制約条件に加えています。ラグランジュ未定乗数法を用いてこの問題を解いてみましょう。ラグランジュ関数Lは以下のようになります。

L = \theta^{T}\Sigma\theta + \lambda(1^{T}\theta - 1)

1階の条件は、

\displaystyle\frac{\partial L}{\partial \theta} = 2\Sigma\theta + 1\lambda = 0 \\ \displaystyle \frac{\partial L}{\partial \lambda} = 1^{T} \theta = 1

1本目の式を\thetaについて解くと、

\theta = \Sigma^{-1}1\lambda^{*}

となります。ここで、\lambda^{*}=-1/2\lambdaです。これを2本目の式に代入し、\lambda^{*}について解きます。

1^{T}\Sigma1\lambda^{*} = 1 \\ \displaystyle \lambda^{*} = \frac{1}{1^{T}\Sigma^{-1}1}

\theta = \Sigma^{-1}1\lambda^{*}だったので、\lambda^{*}を消去すると、

\displaystyle \theta_{gmv} = \frac{\Sigma^{-1}1}{1^{T}\Sigma^{-1}1}

となり、最適なウェイトを求めることができました。とりあえず、これをRで実装しておきます。

# Global Mimimum Variance Portfolio
gmv <- function(r_dat,rcov){
  library(MASS)
  i <- matrix(1,NCOL(r_dat),1)
  r_weight <- (ginv(r_cov)%*%i)/as.numeric(t(i)%*%ginv(r_cov)%*%i)
  wr_dat <- r_dat*as.numeric(r_weight)
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk") 
  return(result)
}

入力は各資産のリターンと分散共分散行列になっています。出力はウェイト、リターン、リスクです。

分散共分散行列をどのように求めるか

最小分散ポートフォリオの計算式は求めることができました。次は、その入力である分散共分散行列をどうやって求めるのかについて分析したいと思います。一番原始的な方法はその時点以前に利用可能なリターンデータを標本として分散共分散行列を求め、その値を固定して最小分散ポートフォリオを求めるというヒストリカルなアプローチかと思います（つまりウェイトも固定）。ただ、これはあくまで過去の平均値を将来の予想値に使用するため、いろいろ問題が出てくるかと思います。専門外の私が思いつくものとしては、前日ある資産Aのリターンが大きく下落したという場面で明日もこの資産の分散は大きくなることが予想されるにも関わらず、平均値を使用するため昨日の効果が薄められてしまうことでしょうか。それに、ウェイトを最初から変更しないというのも時間がたつにつれ、最適点から離れていく気がします。ただ、ではどう推計するのかついてはこの分野でも試行錯誤が行われているようです。Carroll et. al. (2017)でも「The estimation of covariance matrices for portfolios with a large number of assets still remains a fundamental challenge in portfolio optimization.」と述べられていました。この論文では以下のようなモデルを用いて推計が行われています。いずれも、分散共分散行列を時変としているところに特徴があります。

①Constant conditional correlation (CCC) model
元論文はこちら。

https://www.jstor.org/stable/2109358?read-now=1&seq=3#page_scan_tab_contents

まず、分散共分散行列と相関行列の関係性から、\Sigma_{t} = D_{t}R_{t}D_{t}となります。ここで、R_{t}は相関行列、D_{t}はdiag(\sigma_{1,t},...,\sigma_{N,t})で各資産のt期の標準偏差\sigma_{i,t}を対角成分に並べた行列です。ここから、D_{t}とR_{t}を分けて推計していきます。まず、D_{t}ですが、こちらは以下のような多変量GARCHモデル(1,1)で推計します。

r_{t} = \mu + u_{t} \\ u_{t} = \sigma_{t}\epsilon \\ \sigma_{t}^{2} = \alpha_{0} + \alpha_{1}u_{t-1}^{2} + \alpha_{2}\sigma_{t-1}^{2} \\ \epsilon_{t} = NID(0,1) \\ E(u_{t}|u_{t-1}) = 0 \\

ここで、\muはリターンの標本平均です。\alpha_{i}は推定すべきパラメータ。D_{t}をGARCHで推計しているので、リターンの分布が正規分布より裾野の厚い分布に従い、またリターンの変化は一定ではなく前日の分散に依存する関係をモデル化しているといえるのではないでしょうか。とりあえずこれでD_{t}の推計はできたということにします。次にR_{t}の推計ですが、このモデルではリターンを標本として求めるヒストリカルなアプローチを取ります。つまり、R_{t}は定数です。よって、リターン変動の大きさは時間によって変化するが、各資産の相対的な関係性は不変であるという仮定を置いていることになります。

②Dynamic Conditional Correlation (DCC) model
元論文はこちら。

http://www.cass.city.ac.uk/__data/assets/pdf_file/0003/78960/Week7Engle_2002.pdf

こちらのモデルでは、D_{t}を求めるところまでは①と同じですが、R_{t}の求め方が異なっており、ARMA(1,1)を用いて推計します。相関行列はやはり定数ではないということで、t期までに利用可能なリターンを用いて推計をかけようということになっています。このモデルの相関行列R_{t}は、

R_{t} = diag(Q_{t})^{-1/2}Q_{t}diag(Q_{t})^{-1/2}

です。ここで、Q_{t}はt期での条件付分散共分散行列で以下のように定式化されます。

Q_{t} = \bar{Q}(1-a-b) + adiag(Q_{t-1})^{1/2}\epsilon_{i,t-1}\epsilon_{i,t-1}diag(Q_{t-1})^{1/2} + bQ_{t-1}

ここで、\bar{Q}はヒストリカルな方法で計算した分散共分散行列であり、a,bはパラメータです。この方法では、先ほどとは異なり、リターン変動の大きさが時間によって変化するだけでなく、各資産の相対的な関係性も通時的に変化していくという仮定を置いていることになります。金融危機時には全資産のリターンが下落し、各資産の相関が正になる事象も観測されていることから、この定式化は魅力的であるということができるのではないでしょうか。

③Dynamic Equicorrelation (DECO) model
元論文はこちら

https://faculty.chicagobooth.edu/bryan.kelly/research/pdf/deco.pdf

この論文はまだきっちり読めていないのですが、相関行列R_{t}の定義から

R_{t} = (1-\rho_{t})I_{N} + \rho_{t}1

となるようです。ここで、\rho_{t}はスカラーでequicorrelationの程度を表す係数です。equicorrelationとは平均的なペアワイズ相関の事であると理解しています。つまりは欠損値がなければ普通の相関と変わりないんじゃないかと。ただ、資産が増えればそのような問題にも対処する必要があるのでその点ではよい推定量のようです。\rho_{t}は以下のように求めることができます。

\displaystyle \rho_{t} = \frac{1}{N(N-1)}(\iota^{T}R_{t}^{DCC}\iota - N) = \frac{2}{N(N-1)}\sum_{i>j}\frac{q_{ij,t}}{\sqrt{q_{ii,t} q_{jj,t}}}

ここで、\iotaはN×1ベクトルで要素は全て1です。また、q_{ij,t}はQ_{t}のi,j要素です。

さて、分散共分散行列のモデル化ができたところで、ここまでをRで実装しておきます。

carroll <- function(r_dat,FLG){
  
  library(rmgarch)
  
  #1. define variables
  N <- NCOL(r_dat) # the number of assets

  #2. estimate covariance matrix
  basic_garch = ugarchspec(mean.model = list(armaOrder = c(0, 0),include.mean=TRUE), variance.model = list(garchOrder = c(1,1), model = 'sGARCH'), distribution.model = 'norm')
  multi_garch = multispec(replicate(N, basic_garch))
  dcc_set = dccspec(uspec = multi_garch, dccOrder = c(1, 1), distribution = "mvnorm",model = "DCC")
  fit_dcc_garch = dccfit(dcc_set, data = r_dat, fit.control = list(eval.se = TRUE))
  forecast_dcc_garch <- dccforecast(fit_dcc_garch)
  if (FLG == "CCC"){
    #Constant conditional correlation (CCC) model
    D <- sigma(forecast_dcc_garch)
    R_ccc <- cor(r_dat)
    H <- diag(D[,,1])%*%R_ccc%*%diag(D[,,1])
    colnames(H) <- colnames(r_dat)
    rownames(H) <- colnames(r_dat)
  }
  else{
    #Dynamic Conditional Correlation (DCC) model
    H <- as.matrix(rcov(forecast_dcc_garch)[[1]][,,1])
    if (FLG == "DECO"){
      #Dynamic Equicorrelation (DECO) model
      one <- matrix(1,N,N)
      iota <- rep(1,N)
      Q_dcc <- rcor(forecast_dcc_garch,type="Q")[[1]][,,1]
      rho <- as.vector((N*(N-1))^(-1)*(t(iota)%*%Q_dcc%*%iota-N))
      R_deco <- (1-rho)*diag(1,N,N) + rho*one
      D <- sigma(forecast_dcc_garch)
      H <- diag(D[,,1])%*%R_deco%*%diag(D[,,1])
      colnames(H) <- colnames(r_dat)
      rownames(H) <- colnames(r_dat)
    }
  }
  return(H)
}

本来であれば、パッケージを使用するべきではないのですが、今日はエクササイズなので推計結果だけを追い求めたいと思います。GARCHについては再来週ぐらいに記事を書く予定です。
これで準備ができました。この関数にリターンデータを入れて、分散共分散行列を計算し、それを用いて最小分散ポートフォリオを計算することができるようになりました。

テスト用データの収集

データは以下の記事を参考にしました。

www.r-bloggers.com

使用したのは、以下のインデックスに連動するETF(iShares)の基準価額データです。

①S&P500
②NASDAQ100
③MSCI Emerging Markets
④Russell 2000
⑤MSCI EAFE
⑥US 20 Year Treasury(the Barclays Capital 20+ Year Treasury Index)
⑦U.S. Real Estate(the Dow Jones US Real Estate Index)
⑧gold bullion market

library(quantmod)

#**************************
# ★8 ASSETS SIMULATION
# SPY - S&P 500 
# QQQ - Nasdaq 100
# EEM - Emerging Markets
# IWM - Russell 2000
# EFA - EAFE
# TLT - 20 Year Treasury
# IYR - U.S. Real Estate
# GLD - Gold
#**************************

# load historical prices from Yahoo Finance
symbol.names = c("S&P 500","Nasdaq 100","Emerging Markets","Russell 2000","EAFE","20 Year Treasury","U.S. Real Estate","Gold")
symbols = c("SPY","QQQ","EEM","IWM","EFA","TLT","IYR","GLD")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE)

#gn dates for all symbols & convert to monthly
hist.prices = merge(SPY,QQQ,EEM,IWM,EFA,NIK,TLT,IYR,GLD)
month.ends = endpoints(hist.prices, 'day')
hist.prices = Cl(hist.prices)[month.ends, ]
colnames(hist.prices) = symbols

# remove any missing data
hist.prices = na.omit(hist.prices['1995::'])

# compute simple returns
hist.returns = na.omit( ROC(hist.prices, type = 'discrete') )

# compute historical returns, risk, and correlation
ia = list()
ia$expected.return = apply(hist.returns, 2, mean, na.rm = T)
ia$risk = apply(hist.returns, 2, sd, na.rm = T)
ia$correlation = cor(hist.returns, use = 'complete.obs', method = 'pearson')

ia$symbols = symbols
ia$symbol.names = symbol.names
ia$n = length(symbols)
ia$hist.returns = hist.returns

# convert to annual, year = 12 months
annual.factor = 12
ia$expected.return = annual.factor * ia$expected.return
ia$risk = sqrt(annual.factor) * ia$risk

rm(SPY,QQQ,EEM,IWM,EFA,TLT,IYR,GLD)

#install.packages("PerformanceAnalytics")
library(PerformanceAnalytics)

PerformanceAnalytics::charts.PerformanceSummary(hist.returns, main = "パフォーマンスサマリー")

パフォーマンスをまとめたものが以下です。

f:id:osashimix:20190217234849p:plain

バックテストのコーディングを行います。一気にコードを公開します。

#install.packages("quantmod")
#install.packages("rmgarch")
#install.packages("quadprog")

library(quadprog)

carroll <- function(r_dat,FLG){
  
  library(rmgarch)
  
  #1. define variables
  N <- NCOL(r_dat) # the number of assets

  #2. estimate covariance matrix
  basic_garch = ugarchspec(mean.model = list(armaOrder = c(0, 0),include.mean=TRUE), variance.model = list(garchOrder = c(1,1), model = 'sGARCH'), distribution.model = 'norm')
  multi_garch = multispec(replicate(N, basic_garch))
  dcc_set = dccspec(uspec = multi_garch, dccOrder = c(1, 1), distribution = "mvnorm",model = "DCC")
  fit_dcc_garch = dccfit(dcc_set, data = r_dat, fit.control = list(eval.se = TRUE))
  forecast_dcc_garch <- dccforecast(fit_dcc_garch)
  if (FLG == "CCC"){
    #Constant conditional correlation (CCC) model
    D <- sigma(forecast_dcc_garch)
    R_ccc <- cor(r_dat)
    H <- diag(D[,,1])%*%R_ccc%*%diag(D[,,1])
    colnames(H) <- colnames(r_dat)
    rownames(H) <- colnames(r_dat)
  }
  else{
    #Dynamic Conditional Correlation (DCC) model
    H <- as.matrix(rcov(forecast_dcc_garch)[[1]][,,1])
    if (FLG == "DECO"){
      #Dynamic Equicorrelation (DECO) model
      one <- matrix(1,N,N)
      iota <- rep(1,N)
      Q_dcc <- rcor(forecast_dcc_garch,type="Q")[[1]][,,1]
      rho <- as.vector((N*(N-1))^(-1)*(t(iota)%*%Q_dcc%*%iota-N))
      D <- sigma(forecast_dcc_garch)
      R_deco <- (1-rho)*diag(1,N,N) + rho*one
      H <- diag(D[,,1])%*%R_deco%*%diag(D[,,1])
      colnames(H) <- colnames(r_dat)
      rownames(H) <- colnames(r_dat)
    }
  }
  return(H)
}

#define global minimum variance portfolio
gmv <- function(r_dat,r_cov){
  library(MASS)
  i <- matrix(1,NCOL(r_dat),1)
  r_weight <- (ginv(r_cov)%*%i)/as.numeric(t(i)%*%ginv(r_cov)%*%i)
  wr_dat <- r_dat*as.numeric(r_weight)
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk") 
  return(result)
}

nlgmv <- function(r_dat,r_cov){
  qp.out <- solve.QP(Dmat=r_cov,dvec=rep(0,NCOL(r_dat)),Amat=cbind(rep(1,NCOL(r_dat)),diag(NCOL(r_dat))),
           bvec=c(1,rep(0,NCOL(r_dat))),meq=1)
  r_weight <- qp.out$solution
  wr_dat <- r_dat*r_weight
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk")
  return(result)
}

library(quantmod)
library(xts)

#**************************
# ★8 ASSETS SIMULATION
# SPY - S&P 500 
# QQQ - Nasdaq 100
# EEM - Emerging Markets
# IWM - Russell 2000
# EFA - EAFE
# TLT - 20 Year Treasury
# IYR - U.S. Real Estate
# GLD - Gold
#**************************

# load historical prices from Yahoo Finance
symbol.names = c("S&P 500","Nasdaq 100","Emerging Markets","Russell 2000","EAFE","20 Year Treasury","U.S. Real Estate","Gold")
symbols = c("SPY","QQQ","EEM","IWM","EFA","TLT","IYR","GLD")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE)

#gn dates for all symbols & convert to monthly
hist.prices = merge(SPY,QQQ,EEM,IWM,EFA,TLT,IYR,GLD)
month.ends = endpoints(hist.prices, 'day')
hist.prices = Cl(hist.prices)[month.ends, ]
colnames(hist.prices) = symbols

# remove any missing data
hist.prices = na.omit(hist.prices['1995::'])

# compute simple returns
hist.returns = na.omit( ROC(hist.prices, type = 'discrete') )

# compute historical returns, risk, and correlation
ia = list()
ia$expected.return = apply(hist.returns, 2, mean, na.rm = T)
ia$risk = apply(hist.returns, 2, sd, na.rm = T)
ia$correlation = cor(hist.returns, use = 'complete.obs', method = 'pearson')

ia$symbols = symbols
ia$symbol.names = symbol.names
ia$n = length(symbols)
ia$hist.returns = hist.returns

# convert to annual, year = 12 months
annual.factor = 12
ia$expected.return = annual.factor * ia$expected.return
ia$risk = sqrt(annual.factor) * ia$risk

rm(SPY,QQQ,EEM,IWM,EFA,TLT,IYR,GLD)

#install.packages("PerformanceAnalytics")
library(PerformanceAnalytics)

PerformanceAnalytics::charts.PerformanceSummary(hist.returns, main = "パフォーマンスサマリー")

# BACK TEST
backtest <- function(r_dat,FLG,start_date){
  #--------------------------------------
  # BACKTEST
  # r_dat - return data(xts object) 
  # FLG - flag(CCC,DCC,DECO)
  # start_date - start date for backtest
  #--------------------------------------
  
  library(stringi)
  library(tcltk)
  
  initial_dat <- r_dat[stri_c("::",start_date)]
  for (i in NROW(initial_dat):NROW(r_dat)) {
    if (i == NROW(initial_dat)){
      H <- carroll(initial_dat[1:(NROW(initial_dat)-1),],FLG)
      result <- nlgmv(initial_dat,H)
      weight <- t(result$weight)
      colnames(weight) <- colnames(initial_dat)
      p_return <- result$return[NROW(initial_dat),]
      pb <- txtProgressBar(min = NROW(initial_dat), max = NROW(r_dat), style = 3)
    } else {
    if (i %in% endpoints(r_dat,"week")){
      H <- carroll(test_dat[1:(NROW(test_dat)-1),],FLG)
    }
      result <- nlgmv(test_dat,H)
      weight <- rbind(weight,t(result$weight))
      p_return <- rbind(p_return,result$return[NROW(test_dat),])
    }
    if (i != NROW(r_dat)){
      test_dat <- r_dat[1:(i+1),]
    }
    setTxtProgressBar(pb, i)
  }
  p_return.xts <- xts(p_return,order.by = as.Date(row.names(p_return)))
  PerformanceAnalytics::charts.PerformanceSummary(p_return.xts$portfolio
                                                  ,main=stri_c(FLG," BACKTEST"))
  result <- list(p_return.xts,weight)
  names(result) <- c("return","weight")
  return(result)
}

CCC <- backtest(hist.returns,"CCC","2007-01-04")
DCC <- backtest(hist.returns,"DCC","2007-01-04")
DECO <- backtest(hist.returns,"DECO","2007-01-04")

# Equally weighted portfolio
benchmark <- hist.returns*rep(1/NCOL(hist.returns),NCOL(hist.returns))
benchmark <- xts(data.frame(benchmark,apply(benchmark,1,sum)),order.by = index(benchmark))
colnames(benchmark) <- c(colnames(hist.returns),"benchmark")

results <- merge.xts(CCC$return$portfolio,DCC$return$portfolio,DECO$return$portfolio,benchmark$benchmark)
colnames(results) <- c("CCC","DCC","DECO","benchmark")
PerformanceAnalytics::charts.PerformanceSummary(results,main = "BACKTEST")

# plot allocation weighting
d_allocation <- function(result,hist.returns){
  #install.packages("tidyverse")
  library(tidyverse)
  ggweight <- data.frame(result$weight,index(result$return))
  colnames(ggweight) <- c(colnames(hist.returns),"date")
  ggweight <- gather(ggweight,ASSET,weight,colnames(hist.returns))
  ggplot(ggweight, aes(x=date, y=weight,fill=ASSET)) +
    geom_area(colour="black",size=.1)
}

d_allocation(CCC,hist.returns)
d_allocation(DCC,hist.returns)
d_allocation(DECO,hist.returns)

空売り制約を課したので、上で定義した最小分散ポートフォリオは使用していません。どうやらこれだけで解析的に解くのは難しいらしく、数値的に解くことにしています。リバランス期間を週次にしたので、自前のPCでは計算に時間がかかりましたが、結果が計算できました。

f:id:osashimix:20190227222428p:plain

リーマン以降はどうやらベンチマークである等ウェイトポートフォリオよりをアウトパフォームしているようです。特に、DECOはいい感じです。そもそもDECOとDCCはほぼ変わらないパフォーマンスであると思っていたのですが、どうやら自分の理解が足らないらしく、論文の読み返す必要があるようです。Equicorrelationの意味をもう一度考えてみたいと思います。それぞれの組入比率の推移は以下のようになりました。

CCC
f:id:osashimix:20190227232705p:plain

DCC
f:id:osashimix:20190227232803p:plain

DECO
f:id:osashimix:20190227232829p:plain

リーマンの際にTLT、つまり米国債への比率を増やしているようです。CCCとDCCはそれ以外の部分でも米国債への比率が高く、よく挙げられる最小分散ポートフォリオの問題点がここでも発生しているようです。一方、DECOがやはり個性的な組入比率の推移をしており、ここらを考えてももう一度論文を読み返してみる必要がありそうです。
今日はここまで。

追記（2019/3/3）
これまでは、最小分散ポートフォリオで分析をしていましたが、リスクパリティの結果も見たいなと言うことで、そのコードも書いてみました。

#install.packages("quantmod")
#install.packages("rmgarch")
#install.packages("quadprog")

library(quadprog)

carroll <- function(r_dat,FLG){
  
  library(rmgarch)
  
  if(FLG == "benchmark"){
    H <- cov(r_dat)
  }else{
    #1. define variables
    N <- NCOL(r_dat) # the number of assets
    
    #2. estimate covariance matrix
    basic_garch = ugarchspec(mean.model = list(armaOrder = c(0, 0),include.mean=TRUE), variance.model = list(garchOrder = c(1,1), model = 'sGARCH'), distribution.model = 'norm')
    multi_garch = multispec(replicate(N, basic_garch))
    dcc_set = dccspec(uspec = multi_garch, dccOrder = c(1, 1), distribution = "mvnorm",model = "DCC")
    fit_dcc_garch = dccfit(dcc_set, data = r_dat, fit.control = list(eval.se = TRUE))
    forecast_dcc_garch <- dccforecast(fit_dcc_garch)
    if (FLG == "CCC"){
      #Constant conditional correlation (CCC) model
      D <- sigma(forecast_dcc_garch)
      R_ccc <- cor(r_dat)
      H <- diag(D[,,1])%*%R_ccc%*%diag(D[,,1])
      colnames(H) <- colnames(r_dat)
      rownames(H) <- colnames(r_dat)
    }
    else{
      #Dynamic Conditional Correlation (DCC) model
      H <- as.matrix(rcov(forecast_dcc_garch)[[1]][,,1])
      if (FLG == "DECO"){
        #Dynamic Equicorrelation (DECO) model
        one <- matrix(1,N,N)
        iota <- rep(1,N)
        Q_dcc <- rcor(forecast_dcc_garch,type="Q")[[1]][,,1]
        rho <- as.vector((N*(N-1))^(-1)*(t(iota)%*%Q_dcc%*%iota-N))
        D <- sigma(forecast_dcc_garch)
        R_deco <- (1-rho)*diag(1,N,N) + rho*one
        H <- diag(D[,,1])%*%R_deco%*%diag(D[,,1])
        colnames(H) <- colnames(r_dat)
        rownames(H) <- colnames(r_dat)
      }
    }
  }
  return(H)
}

#define global minimum variance portfolio
gmv <- function(r_dat,r_cov){
  library(MASS)
  i <- matrix(1,NCOL(r_dat),1)
  r_weight <- (ginv(r_cov)%*%i)/as.numeric(t(i)%*%ginv(r_cov)%*%i)
  wr_dat <- r_dat*as.numeric(r_weight)
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk") 
  return(result)
}

nlgmv <- function(r_dat,r_cov){
  qp.out <- solve.QP(Dmat=r_cov,dvec=rep(0,NCOL(r_dat)),Amat=cbind(rep(1,NCOL(r_dat)),diag(NCOL(r_dat))),
           bvec=c(1,rep(0,NCOL(r_dat))),meq=1)
  r_weight <- qp.out$solution
  wr_dat <- r_dat*r_weight
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk")
  return(result)
}

risk_parity <- function(r_dat,r_cov){
  fn <- function(weight, r_cov) {
    N <- NROW(r_cov)
    risks <-  weight * (r_cov %*% weight)
    g <- rep(risks, times = N) - rep(risks, each = N)
  return(sum(g^2))
  }
  dfn <- function(weight,r_cov){
    out <- weight
    for (i in 0:length(weight)) {
      up <- dn <- weight
      up[i] <- up[i]+.0001
      dn[i] <- dn[i]-.0001
      out[i] = (fn(up,r_cov) - fn(dn,r_cov))/.0002
    }
    return(out)
  }
  std <- sqrt(diag(r_cov)) 
  x0 <- 1/std/sum(1/std)
  res <- nloptr::nloptr(x0=x0,
                 eval_f=fn,
                 eval_grad_f=dfn,
                 eval_g_eq=function(weight,r_cov) { sum(weight) - 1 },
                 eval_jac_g_eq=function(weight,r_cov) { rep(1,length(std)) },
                 lb=rep(0,length(std)),ub=rep(1,length(std)),
                 opts = list("algorithm"="NLOPT_LD_SLSQP","print_level" = 0,"xtol_rel"=1.0e-8,"maxeval" = 1000),
                 r_cov = r_cov)
  r_weight <- res$solution
  names(r_weight) <- colnames(r_cov)
  wr_dat <- r_dat*r_weight
  portfolio <- apply(wr_dat,1,sum)
  pr_dat <- data.frame(wr_dat,portfolio)
  sd <- sd(portfolio)
  result <- list(r_weight,pr_dat,sd)
  names(result) <- c("weight","return","portfolio risk")
  return(result)
  }

library(quantmod)
library(xts)

#**************************
# ★8 ASSETS SIMULATION
# SPY - S&P 500 
# QQQ - Nasdaq 100
# EEM - Emerging Markets
# IWM - Russell 2000
# EFA - EAFE
# TLT - 20 Year Treasury
# IYR - U.S. Real Estate
# GLD - Gold
#**************************

# load historical prices from Yahoo Finance
#symbol.names = c("S&P 500","Nasdaq 100","Emerging Markets","Russell 2000","EAFE","20 Year Treasury","U.S. Real Estate","Gold")
#symbols = c("SPY","QQQ","EEM","IWM","EFA","TLT","IYR","GLD")
symbol.names <- c("S&P 500","ESCI EM","MSCI EAFE","US AGG","1-3Y TB","Gold","Silver","Real State","WTI")
symbols <- c("IVV","EEM","EFA","AGG","SHY","IAU","SLV","IYR","WTI")
getSymbols(symbols, from = '1980-01-01', auto.assign = TRUE)

#gn dates for all symbols & convert to monthly
#hist.prices = merge(SPY,QQQ,EEM,IWM,EFA,TLT,IYR,GLD)
hist.prices <- merge(IVV,EEM,EFA,AGG,SHY,IAU,SLV,IYR,WTI)
hist.prices = Cl(hist.prices)
colnames(hist.prices) = symbols

# remove any missing data
hist.prices = na.omit(hist.prices['1995::'])

# compute simple returns
hist.returns = na.omit( ROC(hist.prices, type = 'discrete') )


#rm(SPY,QQQ,EEM,IWM,EFA,TLT,IYR,GLD)
rm(IVV,EEM,EFA,AGG,SHY,IAU,SLV,IYR,WTI)

#install.packages("PerformanceAnalytics")
library(PerformanceAnalytics)

PerformanceAnalytics::charts.PerformanceSummary(hist.returns, main = "raw data")


# BACK TEST
backtest <- function(r_dat,FLG,start_date,span,learning_term,port){
  #-----------------------------------------
  # BACKTEST
  # r_dat - return data(xts object) 
  # FLG - flag(CCC,DCC,DECO)
  # start_date - start date for backtest
  # span - rebalance frequency
  # learning_term - learning term (days)
  # port - method of portfolio optimization
  #-----------------------------------------
  
  library(stringi)
  library(tcltk)
  
  initial_dat <- r_dat[stri_c(as.Date(start_date)-learning_term,"::",as.Date(start_date))]
  for (i in NROW(initial_dat):NROW(r_dat)) {
    if (i == NROW(initial_dat)){
      H <- carroll(initial_dat[1:(NROW(initial_dat)-1),],FLG)
      if (port == "nlgmv"){
        result <- nlgmv(initial_dat,H)
      }else if (port == "risk parity"){
        result <- risk_parity(initial_dat,H)
      }
      weight <- t(result$weight)
      colnames(weight) <- colnames(initial_dat)
      p_return <- initial_dat[NROW(initial_dat),]*result$weight
      pb <- txtProgressBar(min = NROW(initial_dat), max = NROW(r_dat), style = 3)
    } else {
      if (i %in% endpoints(r_dat,span)){
        H <- carroll(test_dat[1:(NROW(test_dat)-1),],FLG)
        if (port == "nlgmv"){
          result <- nlgmv(test_dat,H)
        }else if (port == "risk parity"){
          result <- risk_parity(test_dat,H)
        }
      }
      weight <- rbind(weight,t(result$weight))
      p_return <- rbind(p_return,test_dat[NROW(test_dat),]*result$weight)
    }
    if (i != NROW(r_dat)){
      term <- stri_c(index(r_dat[i+1,])-learning_term,"::",index(r_dat[i+1,])) 
      test_dat <- r_dat[term]
    }
    setTxtProgressBar(pb, i)
  }
  p_return$portfolio <- xts(apply(p_return,1,sum),order.by = index(p_return))
  weight.xts <- xts(weight,order.by = index(p_return))
  PerformanceAnalytics::charts.PerformanceSummary(p_return$portfolio
                                                  ,main=stri_c(FLG," BACKTEST"))

  result <- list(p_return,weight.xts)
  names(result) <- c("return","weight")
  return(result)
}

CCC <- backtest(hist.returns,"CCC","2007-01-04","months",365,"risk parity")
DCC <- backtest(hist.returns,"DCC","2007-01-04","months",365,"risk parity")
DECO <- backtest(hist.returns,"DECO","2007-01-04","months",365,"risk parity")
benchmark <- backtest(hist.returns,"benchmark","2007-01-04","months",365,"risk parity")

result <- merge(CCC$return$portfolio,DCC$return$portfolio,DECO$return$portfolio,benchmark$return$portfolio)
colnames(result) <- c("CCC","DCC","DECO","benchmark")
PerformanceAnalytics::charts.PerformanceSummary(result, main = "BACKTEST COMPARISON")

#depict asset allocation
d_allocation <- function(weight){
  #install.packages("tidyverse")
  library(tidyverse)
  ggweight <- data.frame(weight,index(weight))
  colnames(ggweight) <- c(colnames(weight),"date")
  ggweight <- gather(ggweight,ASSET,weight,colnames(weight))
  ggplot(ggweight, aes(x=date, y=weight,fill=ASSET)) +
    geom_area(colour="black",size=.1)
}

# plot allocation weighting
d_allocation(CCC$weight)
d_allocation(DCC$weight)
d_allocation(DECO$weight)
d_allocation(benchmark$weight)

結果はこんな感じ。

f:id:osashimix:20190308053138p:plain

どの手法もbenchmarkをアウトパーフォームできているという好ましい結果になりました。
やはり、分散共分散行列の推計がうまくいっているようです。また、DECOのパフォーマンスがよいのは、相関行列に各資産ペアの相関係数の平均値を用いているため、他の手法よりもリスク資産の組み入れが多くなったからだと思われます。ウェイトは以下の通りです。

CCC
f:id:osashimix:20190308053727p:plain

DCC
f:id:osashimix:20190308053909p:plain

DECO
f:id:osashimix:20190308053930p:plain

benchmark
f:id:osashimix:20190308054022p:plain

とりあえず、今日はここまで。

【日次GDP】カルマンフィルタの実装（R）

おはこんばんにちは。かなり久しぶりの投稿となってしまいました。決して研究をさぼっていたのではなく、BVARのコーディングに手こずっていました。あと少しで完成します。さて、今回はBVARやこの前のGiannnone et a (2008)のような分析でも大活躍のカルマンフィルタを実装してしまいたいと思います。このブログではパッケージソフトに頼らず、基本的に自分で一から実装を行い、研究することをポリシーとしていますので、これから頻繁に使用するであろうカルマンフィルタを関数として実装してしまうことは非常に有益であると考えます。今回はRで実装をしましたので、そのご報告をします。

カルマンフィルタとは？

まず、カルマンフィルタに関する簡単な説明を行います。非常にわかりやすい記事があるので、そちらを読んでいただいたほうがより分かりやすいかと思います。

qiita.com

カルマンフィルタとは、状態空間モデルを解くアルゴリズムの一種です。状態空間モデルとは、手元の観測可能な変数から観測できない変数を推定するモデルであり、以下のような形をしています。

Y_{t} = Z_{t}\alpha_{t} + d_{t} + S_{t}\epsilon_{t} \\ \alpha_{t} = T_{t}\alpha_{t-1} + c_{t} + R_{t}\eta_{t}

ここで、 Y_{t}はg×1ベクトルの観測可能な変数(観測変数)、 Z_{t}はg×k係数行列、 \alpha_{t}はk×1ベクトルの観測不可能な変数(状態変数)、 T_{t}はk×k係数行列です。また、 \epsilon_{t}は観測変数の誤差項、 \eta_{t}は状態変数の誤差項です。これらの誤差項はそれぞれN(0,H_{t}), N(0,Q_{t})に従います（H_{t}, Q_{t}は分散共分散行列）。d_{t}, c_{t}は定数項です。1本目の式は観測方程式、2本目の式は遷移方程式と呼ばれます。
状態空間モデルを使用する例として、しばしば池の魚の数を推定する問題が使用されます。今、池の中の魚の全数が知りたいとして、その推定を考えます。観測時点毎に池の中の魚をすべて捕まえてその数を調べるのは現実的に困難なので、一定期間釣りをして釣れた魚をサンプルに全数を推定することを考えます。ここで、釣れた魚は観測変数、池にいる魚の全数は状態変数と考えることができます。今、経験的に釣れた魚の数と全数の間に以下のような関係があるとします。

Y_{t} = 0.01\alpha_{t} + 5 + \epsilon_{t}

これが観測方程式になります。また、魚の全数は過去の値からそれほど急速には変化しないと考えられるため、以下のようなランダムウォークに従うと仮定します。

\alpha_{t} = \alpha_{t-1} + 500 + \eta_{t}

これが遷移方程式になります。あとは、これをカルマンフィルタアルゴリズムを用いて計算すれば、観測できない魚の全数を推定することができます。
このように状態空間モデルは非常に便利なモデルであり、また応用範囲も広いです。例えば、販売額から潜在顧客数を推定したり、クレジットスプレッドやトービンのQ等経済モデル上の概念として存在する変数を推定する、BVARのようにVARや回帰式の時変パラメータ推定などにも使用されます。

カルマンフィルタアルゴリズムの導出

さて、非常に便利な状態空間モデルの説明はこれくらいにして、カルマンフィルタの説明に移りたいと思います。カルマンフィルタは状態空間モデルを解くアルゴリズムの一種であると先述しました。つまり、他にも状態空間モデルを解くアルゴリズムは存在します。カルマンフィルタアルゴリズムは一般に誤差項の正規性の仮定を必要としないフィルタリングアルゴリズムであり、観測方程式と遷移方程式の線形性の仮定さえあれば、線形最小分散推定量となります。カルマンフィルタアルゴリズムの導出にはいくつかの方法がありますが、今回はこの線形最小分散推定量としての導出を行います。まず、以下の３つの仮定を置きます。

①初期値\alpha_{0}は正規分布N(a_{0},\Sigma_{0})に従う確率ベクトルである(a_{t}は\alpha_{t}の推定値)。
②誤差項\epsilon_{t},\eta_{s}は全てのt,sで互いに独立で、初期値ベクトル\alpha_{0}と無相関である（E(\epsilon_{t}\eta_{s}')=0, E(\epsilon_{t}\alpha_{0}')=0, E(\eta_{t}\alpha_{0}')=0）。
③②より、E(\epsilon_{t}\alpha_{t}')=0、E(\eta_{t}\alpha_{t-1}')=0。

まず、t-1期の情報集合\Omega_{t-1}が既知の状態での\alpha_{t}とY_{t}の期待値（予測値）を求めてみましょう。上述した状態空間モデルと誤差項の期待値がどちらもゼロである事実を用いると、以下のように計算することができます。

E(\alpha_{t}|\Omega_{t-1}) = a_{t|t-1} = T_{t}a_{t-1|t-1} + c_{t}
E(Y_{t}|\Omega_{t-1}) = Y_{t|t-1} = Z_{t}a_{t|t-1} + d_{t}

ここで、次に、これらの分散を求めます。
E( (\alpha_{t}-a_{t|t-1})(\alpha_{t}-a_{t|t-1})'|\Omega_{t-1}) = E( (T_{t}\alpha_{t-1} + c_{t} + R_{t}\eta_{t}-a_{t|t-1})(T_{t}\alpha_{t-1} + c_{t} + R_{t}\eta_{t}-a_{t|t-1})'|\Omega_{t-1}) \\ = E(T_{t}\alpha_{t-1}\alpha_{t-1}'T_{t}' + R_{t}\eta_{t}\eta_{t}'R_{t}'|\Omega_{t-1}) = E(T_{t}\alpha_{t-1}\alpha_{t-1}'T_{t}'|\Omega_{t-1}) + E(R_{t}\eta_{t}\eta_{t}'R_{t}'|\Omega_{t-1}) \\ = T_{t}E(\alpha_{t-1}\alpha_{t-1}'|\Omega_{t-1})T_{t}' + R_{t}E(\eta_{t}\eta_{t}'|\Omega_{t-1})R_{t}' = T_{t}\Sigma_{t-1|t-1}T_{t}' + R_{t}Q_{t}R_{t}' \\ = \Sigma_{t|t-1}

E( (Y_{t}-Y_{t|t-1})(Y_{t}-Y_{t|t-1})'|\Omega_{t-1}) = E( (Z_{t}\alpha_{t} + d_{t} + S_{t}\epsilon_{t}-Y_{t|t-1})(Z_{t}\alpha_{t} + d_{t} + S_{t}\epsilon_{t}-Y_{t|t-1})'|\Omega_{t-1}) \\ = E(Z_{t}\alpha_{t}\alpha_{t}'Z_{t}' + S_{t}\epsilon_{t}\epsilon_{t}'S_{t}'|\Omega_{t-1}) = E(Z_{t}\alpha_{t}\alpha_{t}'Z_{t}'|\Omega_{t-1}) + E(S_{t}\epsilon_{t}\epsilon_{t}'S_{t}'|\Omega_{t-1}) \\ = Z_{t}E(\alpha_{t}\alpha_{t}'|\Omega_{t-1})Z_{t}' + S_{t}E(\epsilon_{t}\epsilon_{t}'|\Omega_{t-1})S_{t}' = Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}' \\ = F_{t|t-1}

ここで、t期の情報集合\Omega_{t}が得られたとします（つまり、観測値Y_{t}を入手）。カルマンフィルタでは、t期の情報である観測値Y_{t}を用いてa_{t|t-1}を以下の方程式で更新します。

E(\alpha_{t}|\Omega_{t}) = a_{t|t} = a_{t|t-1} + k_{t}(Y_{t} - Y_{t|t-1})

つまり、観測値とY_{t}の期待値（予測値）の差をあるウェイトk_{t}（k×g行列）でかけたもので補正をかけるわけです。よって、観測値と予測値が完全に一致していた場合は補正は行われないことになります。ここで重要なのは、ウエイトk_{t}をどのように決めるのかです。k_{t}は更新後の状態変数の分散 E( (\alpha_{t} - a_{t|t})(\alpha_{t} - a_{t|t})')= \Sigma_{t|t}を最小化するよう決定します。これが、カルマンフィルタが線形最小分散推定量である根拠です。最小化にあたっては以下のベクトル微分が必要になりますので、おさらいをしておきましょう。今回使用するのは以下の事実です。

\displaystyle \frac{\partial a'b}{\partial b} = \frac{\partial b'a}{\partial b} = a \\ \displaystyle \frac{\partial b'Ab}{\partial b} = 2Ab

ここで、a,bはベクトル（それぞれn×1ベクトル、1×nベクトル）、Aはn×nの対称行列です。まず、１つ目から証明していきます。\displaystyle y = a'b = b'a = \sum_{i=1}^{n}a_{i}b_{i}とします。
このとき、 \frac{\partial y}{\partial b_{i}}=a_{i}なので、

\displaystyle \frac{\partial a'b}{\partial b} = \frac{\partial b'a}{\partial b} = a

次に２つ目です。y = b'Ab = \sum_{i=1}^{n}\sum_{j=1}^{n}a_{ij}b_{i}b_{j}とします。このとき、

\displaystyle \frac{\partial y}{\partial b_{i}} = \sum_{j=1}^{n}a_{ij}b_{j} + \sum_{j=1}^{n}a_{ji}b_{j} = 2\sum_{j=1}^{n}a_{ij}b_{j} = 2a_{i}'b

よって、

\displaystyle \frac{\partial y}{\partial b} = \left( \begin{array}{cccc} \frac{\partial y}{\partial b_{1}} \\ \vdots \\ \frac{\partial y}{\partial b_{n}} \\ \end{array} \right) = 2 \left( \begin{array}{cccc} \sum_{j=1}^{n}a_{1j}b_{j} \\ \vdots \\ \sum_{j=1}^{n}a_{nj}b_{j} \\ \end{array} \right) = 2 \left( \begin{array}{cccc} a_{1}'b \\ \vdots \\ a_{n}'b \\ \end{array} \right) = 2Ab

さて、準備ができたので、更新後の状態変数の分散 E( (\alpha_{t} - a_{t|t})(\alpha_{t} - a_{t|t})')を求めてみましょう。

E( (\alpha_{t} - a_{t|t})(\alpha_{t} - a_{t|t})') = \Sigma_{t|t} = E\{ (\alpha_{t} - a_{t|t-1} + k_{t}(Y_{t} - Y_{t|t-1}))(\alpha_{t} - a_{t|t-1} + k_{t}(Y_{t} - Y_{t|t-1}))'\} \\ = E\{ ( (\alpha_{t} - a_{t|t-1}) - k_{t}(Z_{t}\alpha_{t} + d_{t} + S_{t}\epsilon_{t} - Z_{t}a_{t|t-1} - d_{t}) )( (\alpha_{t} - a_{t|t-1}) - k_{t}(Z_{t}\alpha_{t} + d_{t} + S_{t}\epsilon_{t} - Z_{t}a_{t|t-1} - d_{t}) )\} \\ = E\{ ( (\alpha_{t} - a_{t|t-1}) - k_{t}(Z_{t}\alpha_{t} + S_{t}\epsilon_{t} - Z_{t}a_{t|t-1}) )( (\alpha_{t} - a_{t|t-1}) - k_{t}(Z_{t}\alpha_{t} + S_{t}\epsilon_{t} - Z_{t}a_{t|t-1}) )'\} \\ = E\{ ( (I - k_{t}Z_{t})\alpha_{t} - k_{t}S_{t}\epsilon_{t} - (I - k_{t}Z_{t})a_{t|t-1})( (I - k_{t}Z_{t})\alpha_{t} - k_{t}S_{t}\epsilon_{t} - (I - k_{t}Z_{t})a_{t|t-1})' \} \\ = E\{( (I - k_{t}Z_{t})(\alpha_{t}-a_{t|t-1}) - k_{t}S_{t}\epsilon_{t})( (I - k_{t}Z_{t})(\alpha_{t}-a_{t|t-1}) - k_{t}S_{t}\epsilon_{t})'\} \\ = (I - k_{t}Z_{t})\Sigma_{t|t-1}(I - k_{t}Z_{t})' + k_{t}S_{t}H_{t}S_{t}'k_{t}' \\ = (\Sigma_{t|t-1} - k_{t}Z_{t}\Sigma_{t|t-1})(I - k_{t}Z_{t})' + k_{t}S_{t}H_{t}S_{t}'k_{t}' \\ = \Sigma_{t|t-1} - \Sigma_{t|t-1}(k_{t}Z_{t})' - k_{t}Z_{t}\Sigma_{t|t-1} + k_{t}Z_{t}\Sigma_{t|t-1}Z_{t}'k_{t}' + k_{t}S_{t}H_{t}S_{t}'k_{t}' \\ = \Sigma_{t|t-1} - \Sigma_{t|t-1}Z_{t}'k_{t}' - k_{t}Z_{t}\Sigma_{t|t-1} + k_{t}(Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}')k_{t}' \\

１回目の式変形で、a_{t|t}に上述した更新式を代入し、２回目の式変形で観測方程式と上で計算した E(Y_{t}|\Omega_{t-1})を代入しています。さて、更新後の状態変数の分散\Sigma_{t|t}をk_{t}の関数として書き表すことができたので、これをk_{t}で微分し、0と置き、\Sigma_{t|t}を最小化するk_{t}を求めます。先述した公式で、a=\Sigma_{t|t-1}Z_{t}'、b=k_{t}'、A=(Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}')とすると（Aは分散共分散行列の和なので対称行列）、

\frac{\partial \Sigma_{t|t}}{\partial k_{t}'} = -2(Z_{t}\Sigma_{t|t-1})' + 2(Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}')k_{t} = 0

ここから、k_{t}を解きなおすと、

k_{t} = \Sigma_{t|t-1}Z_{t}'(Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}')^{-1} \\ = \Sigma_{t|t-1}Z_{t}'F_{t|t-1}^{-1}

突然、F_{t|t-1}が出てきました。これは観測変数の予測値の分散 E( (Y_{t}-Y_{t|t-1})(Y_{t}-Y_{t|t-1})'|\Omega_{t-1})でした。一方、\Sigma_{t|t-1}Z_{t}は状態変数の予測値の分散を観測変数のスケールに調整したものです（観測空間に写像したもの）。つまり、カルマンゲインk_{t}は状態変数と観測変数の予測値の分散比となっているのです。観測変数にはノイズがあり、観測方程式はいつも誤差０で満たされるわけではありません。また、状態方程式にも誤差項が存在します。状態の遷移も100%モデル通りにはいかないということです。t期の観測変数Y_{t}が得られたとして、それをどれほど信頼して状態変数を更新するかは観測変数のノイズが状態変数のノイズに比べてどれほど小さいかによります。つまり、相対的に観測方程式が遷移方程式よりも信頼できる場合には状態変数を大きく更新するのです。このように、カルマンフィルタでは、観測方程式と遷移方程式の相対的な信頼度によって、更新の度合いを毎期調整しています。その度合いが分散比であり、カルマンゲインだというわけです。ちなみに欠損値が発生した場合には、観測変数の分散を無限大にし、状態変数の更新を全く行わないという対処を行います。観測変数に信頼がないので当たり前の処置です。この場合は遷移方程式を100%信頼します。これがカルマンフィルタのコアの考え方になります。
更新後の分散を計算しておきます。

\Sigma_{t|t} = \Sigma_{t|t-1} - \Sigma_{t|t-1}Z_{t}'k_{t}' - k_{t}Z_{t}\Sigma_{t|t-1} + k_{t}F_{t|t-1}k_{t}' \\ = \Sigma_{t|t-1} - \Sigma_{t|t-1}Z_{t}'k_{t}' - k_{t}Z_{t}\Sigma_{t|t-1} + (\Sigma_{t|t-1}Z_{t}'F_{t|t-1}^{-1})F_{t|t-1}k_{t}' \\ = \Sigma_{t|t-1} - \Sigma_{t|t-1}Z_{t}'k_{t}' - k_{t}Z_{t}\Sigma_{t|t-1} + \Sigma_{t|t-1}Z_{t}'k_{t}' \\ = \Sigma_{t|t-1} - k_{t}Z_{t}\Sigma_{t|t-1} \\ = \Sigma_{t|t-1} - k_{t}F_{t|t-1}F_{t|t-1}^{-1}Z_{t}\Sigma_{t|t-1} \\ = \Sigma_{t|t-1} - k_{t}F_{t|t-1}k_{t}'

では、最終的に導出されたアルゴリズムをまとめたいと思います。

a_{t|t-1} = T_{t}a_{t-1|t-1} + c_{t} \\ \Sigma_{t|t-1} = T_{t}\Sigma_{t-1|t-1}T_{t}' + R_{t}Q_{t}R_{t}' \\ Y_{t|t-1} = Z_{t}a_{t|t-1} + d_{t} \\ F_{t|t-1} = Z_{t}\Sigma_{t|t-1}Z_{t}' + S_{t}H_{t}S_{t}' \\ k_{t} = \Sigma_{t|t-1}Z_{t}'F_{t|t-1}^{-1} \\ a_{t|t} = a_{t|t-1} + k_{t}(Y_{t} - Y_{t|t-1}) \\ \Sigma_{t|t} = \Sigma_{t|t-1} - k_{t}F_{t|t-1}k_{t}'

初期値a_{0},\Sigma_{0}が所与の元で、まず状態変数の予測値a_{1|0},\Sigma_{1|0}を計算します。その結果を用いて、次は観測変数の予測値Y_{t|t-1},F_{t|t-1}を計算し、カルマンゲインk_{t}を得ます。t期の観測可能なデータを入手したら、更新方程式を用いてa_{t|t},\Sigma_{t|t}を更新します。これをサンプル期間繰り返していくことになります。ちなみに、遷移方程式の誤差項\eta_{t}と定数項c_{t}がなく、遷移方程式のパラメータが単位行列のカルマンフィルタは逐次最小自乗法と一致します。つまり、新しいサンプルを入手するたびにOLSをやり直す推計方法ということです（今回はその証明は勘弁してください）。

Rで実装する。

以下がRでの実装コードです。

#Kalman filter

kalmanfiter <- function(y,I,t,z,c=0,R=NA,Q=NA,d=0,S=NA,h=NA,a_int=NA,sig_int=NA){
  #-------------------------------------------------------------------
  # Implemention of Kalman filter
  #   y - observed variable
  #   I - the number of unobserved variable
  #   t - parameter of endogenous variable in state equation
  #   z - parameter of endogenous variable in observable equation
  #   c - constant in state equaion
  #   R - parameter of exogenous variable in state equation
  #   Q - var-cov matrix of exogenous variable in state equation
  #   d - constant in observable equaion
  #   S - parameter of exogenous variable in observable equation
  #   h - var-cov matrix of exogenous variable in observable equation
  #   a_int - initial value of endogenous variable
  #   sig_int - initial value of variance of endogenous variable
  #-------------------------------------------------------------------
  
  library(MASS)
    
  # 1.Define Variable
  if (class(y)!="matrix"){
    y <- as.matrix(y)
  }
  N <- NROW(y) # sample size
  L <- NCOL(y) # the number of observable variable 
  a_pre <- array(0,dim = c(I,1,N)) # prediction of unobserved variable
  a_fil <- array(0,dim = c(I,1,N+1)) # filtered of unobserved variable
  sig_pre <- array(0,dim = c(I,I,N)) # prediction of var-cov mat. of unobserved variable
  sig_fil <- array(0,dim = c(I,I,N+1)) # filtered of var-cov mat. of unobserved variable
  y_pre <- array(0,dim = c(L,1,N)) # prediction of observed variable
  F_pre <- array(0,dim = c(L,L,N)) # auxiliary variable 
  k <- array(0,dim = c(I,L,N)) # kalman gain
  
  if (is.na(a_int)==TRUE){
    a_int <- matrix(0,nrow = I,ncol = 1)
  }
  if (is.na(sig_int)==TRUE){
    sig_int <- diag(1,nrow = I,ncol = I)
  }
  if (is.na(R)==TRUE){
    R <- diag(1,nrow = I,ncol = I)
  }
  if (is.na(Q)==TRUE){
    Q <- diag(1,nrow = I,ncol = I)
  }
  if (is.na(S)==TRUE){
    S <- matrix(1,nrow = L,ncol = L)
  }
  if (is.na(h)==TRUE){
    H <- array(0,dim = c(L,L,N))
    for(i in 1:N){
      diag(H[,,i]) = 1
    }
  }else if (class(h)!="array"){
    H <- array(h,dim = c(NROW(h),NCOL(h),N))
  }
  
  # fill infinite if observed data is NA
  for(i in 1:N){
    miss <- is.na(y[i,])
    diag(H[,,i])[miss] <- 1e+32
  }
  y[is.na(y)] <- 0  

  # 2.Set Initial Value
  a_fil[,,1] <- a_int
  sig_fil[,,1] <- sig_int
  
  # 3.Implement Kalman filter
  for (i in 1:N){
    if(class(z)=="array"){
      Z <- z[,,i]
    }else{
      Z <- z
    }
    a_pre[,,i] <- t%*%a_fil[,,i] + c
    sig_pre[,,i] <- t%*%sig_fil[,,i]%*%t(t) + R%*%Q%*%t(R)
    y_pre[,,i] <- Z%*%a_pre[,,i] + d
    F_pre[,,i] <- Z%*%sig_pre[,,i]%*%t(Z) + S%*%H[,,i]%*%t(S)
    k[,,i] <- sig_pre[,,i]%*%t(Z)%*%ginv(F_pre[,,i])
    a_fil[,,i+1] <- a_pre[,,i] + k[,,i]%*%(y[i,]-y_pre[,,i])
    sig_fil[,,i+1] <- sig_pre[,,i] - k[,,i]%*%F_pre[,,i]%*%t(k[,,i])
  }
  
  # 4.Aggregate results
  result <- list(a_pre,a_fil,sig_pre,sig_fil,y_pre,k)
  names(result) <- c("state prediction", "state filtered", "state var prediction", 
                     "state var filtered", "observable prediction", "kalman gain")
  return(result)
}

案外簡単に書けるもんですね。これを使って、Giannone et al (2008)をやり直してみます。過去記事はこちら。

osashimix.hatenablog.com

データセットは前回記事と変わりません。データの収集方法はこちら。

osashimix.hatenablog.com

以下、分析用のRコードです。

#------------------------
# Giannone et. al. 2008 
#------------------------

# ファクターを計算
f <- 3　# the number of factors
z <- scale(dataset1) # データセットを標準化
for (i in 1:nrow(z)){
  eval(parse(text = paste("S_i <- z[i,]%*%t(z[i,])",sep = "")))
  if (i==1){
    S <- S_i
  }else{
    S <- S + S_i
  }
}
S <- (1/nrow(z))*S
gamma <- eigen(S)
D <- diag(gamma$values[1:f])
V <- gamma$vectors[,1:f] #固有ベクトルを抽出
F_t <- matrix(0,nrow(z),f)
for (i in 1:nrow(z)){
  eval(parse(text = paste("F_t[",i,",]<- z[",i,",]%*%V",sep = ""))) #主成分分析にてファクターを計算（カルマンフィルタの初期値に使用）
}
lambda_hat <- V #観測方程式の係数行列
R <- diag(diag(cov(z-z%*%V%*%t(V)))) #観測方程式の分散共分散行列 

a <- matrix(0,f,f)
b <- matrix(0,f,f)
for(t in 2:nrow(z)){
  a <- a + F_t[t,]%*%t(F_t[t-1,])
  b <- b + F_t[t-1,]%*%t(F_t[t-1,])
}
b_inv <- solve(b)
A_hat <- a%*%b_inv #VAR推計

e <- numeric(f)
for (t in 2:nrow(F_t)){
  e <- e + F_t[t,]-F_t[t-1,]%*%A_hat
}
H <- t(e)%*%e
Q <- diag(1,f,f)
Q[1:f,1:f] <- H #遷移方程式の分散共分散行列

a <- which(dataset$publication == "1980-01-01")
dataset2 <- dataset[a:nrow(dataset),]
rownames(dataset2) <- dataset2$publication
dataset2 <- dataset2[,-2]
zz <- scale(dataset2)
p <- ginv(diag(nrow(kronecker(A_hat,A_hat)))-kronecker(A_hat,A_hat))

result1 <- kalmanfiter(zz,f,A_hat,V,c=0,R=NA,Q=Q,d=0,S=NA,h=psi,a_int=F_t[1,],sig_int=matrix(p,f,f))
F_tk <- xts(t(result1$`state filtered`[,1,305:469]),order.by = as.Date(rownames(dataset2[305:469,])))
plot.zoo(F_tk,col = c("red","blue","green"),plot.type = "single",ylab = "factor",xlab = "time")

出力されたグラフが以下です。

f:id:osashimix:20190211234917p:plain

giannoneの記事を書いた際は、元論文のMATLABコードを参考にRで書いたのですが、通常のカルマンフィルタとは観測変数の分散共分散行列の逆数の計算方法が違うらしくグラフの形が異なっています。まあでも、概形はほとんど同じですが（なので、ちゃんと動いているはず）。

カルマンスムージング

カルマンフィルタの実装は以上で終了なのですが、誤差項の正規性を仮定すればT期までの情報集合\Omega_{T}を用いて、a_{i|i}, \Sigma_{i|i}(i = 1:T)をa_{i|T}, \Sigma_{i|T}(i = 1:T)へ更新することができます。これをカルマンスムージングと呼びます。これを導出してみましょう。その準備として、以下のような\alpha_{t|t}と\alpha_{t+1|t}の混合分布を計算しておきます。

(\alpha_{t|t},\alpha_{t+1|t}) = N( \left( \begin{array}{cccc} E(\alpha_{t|t}) \\ E(\alpha_{t+1|t}) \end{array} \right), \left( \begin{array}{cccc} Var(\alpha_{t|t}), Cov(\alpha_{t|t},\alpha_{t+1|t}) \\ Cov(\alpha_{t+1|t},\alpha_{t|t}), Var(\alpha_{t+1|t}) \end{array} \right) ) \\ = N( \left( \begin{array}{cccc} a_{t|t} \\ a_{t+1|t} \end{array} \right), \left( \begin{array}{cccc} \Sigma_{t|t}, \Sigma_{t|t}T_{t}' \\ T_{t}\Sigma_{t|t}, \Sigma_{t+1|t} \end{array} \right) )

ここで、Cov(\alpha_{t|t},\alpha_{t+1|t})は

Cov(\alpha_{t+1|t},\alpha_{t|t}) = Cov(T_{t}\alpha_{t-1} + c_{t} + R_{t}\eta_{t}, \alpha_{t|t}) \\ = T_{t}Cov(\alpha_{t|t},\alpha_{t|t}) + Cov(c_{t},\alpha_{t|t}) + Cov(R_{t}\eta_{t},\alpha_{t|t}) \\ = T_{t}Var(\alpha_{t|t}) = T_{t}\Sigma_{t|t}

ここで、条件付き多変量正規分布は以下のような分布をしていることを思い出しましょう（
多変量正規分布における条件付き確率の式と意味 - 具体例で学ぶ数学
）。

(X_{1},X_{2}) = N( \left( \begin{array}{cccc} \mu_{1} \\ \mu_{2} \end{array} \right), \left( \begin{array}{cccc} \Sigma_{11}, \Sigma_{12} \\ \Sigma_{21}, \Sigma_{22} \end{array} \right) ) \\

(X_{1}|X_{2}=x_{2}) = N(\mu_{1} + \Sigma_{12}\Sigma_{22}^{-1}(x_{2}-\mu_{2}),\Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21})

これを用いて、(\alpha_{t|t}|\alpha_{t+1|t}=a_{t+1})を計算してみましょう。

(\alpha_{t|t}|\alpha_{t+1|t}=a_{t+1}) = N(a_{t|t} + \Sigma_{t|t}T_{t}'\Sigma_{t+1|t}^{-1}(a_{t+1}-a_{t+1|t}), \Sigma_{t|t}-\Sigma_{t|t}T_{t}'\Sigma_{t+1|t}^{-1}T_{t}\Sigma_{t|t}) \\ =N(a_{t|t} + L_{t}(a_{t+1}-a_{t+1|t}), \Sigma_{t|t}-L_{t}\Sigma_{t+1|t}L_{t}')

ただし、a_{t+1}の値は観測不可能なので、上式を用いて状態変数を更新することはできません。今、わかるのはT期におけるa_{t+1|T}の分布のみです。ということで、a_{t+1}をa_{t+1|T}で代用し、\alpha_{t|T}の分布を求めてみます。では、計算していきます。\alpha_{t|T} = N(E(\alpha_{t|T}),Var(\alpha_{t|T}))ですが、

E(\alpha_{t|T}) = E_{\alpha_{t+1|T}}(E(\alpha_{t|t}|\alpha_{t+1|t}=\alpha_{t+1|T})) \\ Var(\alpha_{t|T}) = E_{\alpha_{t+1|T}}(Var(\alpha_{t|t}|\alpha_{t+1|t} = \alpha_{t+1|T})) + Var_{\alpha_{t+1|T}}(E(\alpha_{t|t}|\alpha_{t+1|t}=\alpha_{t+1|T}))

というように、\alpha_{t+1|T}も確率変数となるので、繰り返し期待値の法則と繰り返し分散の法則を使用します（こちらを参照）。

繰り返し期待値の法則
E(x) = E_{Z}(E(X|Y=Z))

繰り返し分散の法則
Var(X) = E_{Z}(Var(X|Y=Z))+Var_{Z}(E(X|Y=Z))

よって、

E(\alpha_{t|T}) = E_{\alpha_{t+1|T}}(E(\alpha_{t|t}|\alpha_{t+1|t}=\alpha_{t+1|T})) = a_{t|t} + L_{t}(a_{t+1|T}-a_{t+1|t}) \\ Var(\alpha_{t|T}) = E_{\alpha_{t+1|T}}(Var(\alpha_{t|t}|\alpha_{t+1|t} = \alpha_{t+1|T})) + Var_{\alpha_{t+1|T}}(E(\alpha_{t|t}|\alpha_{t+1|t}=\alpha_{t+1|T})) \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + E( (a_{t|t} + L_{t}(\alpha_{t+1|T}-a_{t+1|t}) - a_{t|t} - L_{t}(a_{t+1|T}-a_{t+1|t}))(a_{t|t} + L_{t}(\alpha_{t+1|T}-a_{t+1|t}) - a_{t|t} - L_{t}(a_{t+1|T}-a_{t+1|t}))') \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + E( (L_{t}(\alpha_{t+1|T}-a_{t+1|t}) - L_{t}(a_{t+1|T}-a_{t+1|t}))(L_{t}(\alpha_{t+1|T}-a_{t+1|t}) - L_{t}(a_{t+1|T}-a_{t+1|t}))') \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + E( (L_{t}\alpha_{t+1|T} - L_{t}a_{t+1|T})(L_{t}\alpha_{t+1|T} - L_{t}(a_{t+1|T})') \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + E( L_{t}(\alpha_{t+1|T} - a_{t+1|T})(\alpha_{t+1|T} - a_{t+1|T})'L_{t}') \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + L_{t}E( (\alpha_{t+1|T} - a_{t+1|T})(\alpha_{t+1|T} - a_{t+1|T})')L_{t}' \\ = \Sigma_{t|t} - L_{t}\Sigma_{t+1|t}L_{t}' + L_{t}\Sigma_{t+1|T}L_{t}'

となります。カルマンスムージングのアルゴリズムをまとめておきます。

L_{t} = \Sigma_{t|t}T_{t}\Sigma_{t+1|t}^{-1} \\ a_{t|T} = a_{t|t} + L_{t}(a_{t+1|T} - a_{t+1|t}) \\ \Sigma_{t|T} = \Sigma_{t+1|t} + L_{t}(\Sigma_{t+1|T}-\Sigma_{t+1|t})L_{t}'

カルマンスムージングの特徴的な点は後ろ向きに計算をしていく点です。つまり、T期から1期に向けて計算を行っていきます。L_{t}に関してはそもそもカルマンフィルタを回した時点で計算可能ですが、\alpha_{t|T}はT期までのデータが手元にないと計算できません。今、T期まで観測可能なデータが入手できたとしましょう。すると、２番目の方程式を用いて、a_{T-1|T}を計算します。ちなみにa_{T|T}はカルマンフィルタを回した時点ですでに手に入っているので、計算する必要はありません。同時に、３番目の式を用いて\Sigma_{T-1|T}を計算します。そして、a_{T-1|T},\Sigma_{T-1|T}とL_{T-1}を用いてa_{T-2|T},\Sigma_{T-2|T}を計算、というように1期に向けて後ろ向きに計算をしていくのです。さきほど、遷移方程式の誤差項\eta_{t}と定数項c_{t}がなく、遷移方程式のパラメータが単位行列のカルマンフィルタは逐次最小自乗法と一致すると書きましたが、カルマンスムージングの場合はT期までのサンプルでOLSを行った結果と一致します。
Rで実装してみます。

kalmansmoothing <- function(filter){
  #-------------------------------------------------------------------
  # Implemention of Kalman smoothing
  #   t - parameter of endogenous variable in state equation
  #   z - parameter of endogenous variable in observable equation
  #   a_pre - prediction of state
  #   a_fil - filtered value of state
  #   sig_pre - prediction of var of state
  #   sig_fil - filtered value of state
  #-------------------------------------------------------------------
  
  library(MASS)
  
  # 1.Define variable
  a_pre <- filter$`state prediction`
  a_fil <- filter$`state filtered`
  sig_pre <- filter$`state var prediction`
  sig_fil <- filter$`state var filtered`
  t <- filter$`parameter of state eq`
  C <- array(0,dim = dim(sig_fil))
  a_sm <- array(0,dim = dim(a_fil))
  sig_sm <- array(0,dim = dim(sig_fil))
  N <- dim(C)[3]
  a_sm[,,N] <- a_fil[,,N]
  sig_sm[,,N] <- sig_fil[,,N]
  
  for (i in dim(C)[3]:2){
    C[,,i-1] <- sig_fil[,,i-1]%*%t(t)%*%ginv(sig_pre[,,i])
    a_sm[,,i-1] <- a_fil[,,i-1] + C[,,i-1]%*%(a_sm[,,i]-a_pre[,,i])
    sig_sm[,,i-1] <- sig_fil[,,i-1] + C[,,i-1]%*%(sig_sm[,,i]-sig_pre[,,i])%*%t(C[,,i-1])
  }
  
  
  result <- list(a_sm,sig_sm,C)
  names(result) <- c("state smoothed", "state var smoothed", "c")
}

先ほどのコードの続きでRコードを書いてみます。

result2 <- kalmansmoothing(result1)

かなりシンプルですね。ちなみにグラフにしましたが、１個目とほぼ変わりませんでした。とりあえず、今日はここまで。

【日次GDP】ガウス回帰の実装をやってみた

おはこんばんにちは。昨日、Bayesian Vector Autoregressionの記事を書きました。

osashimix.hatenablog.com

その中でハイパーパラメータのチューニングの話が出てきて、なにか効率的にチューニングを行う方法はないかと探していた際にBayesian Optimizationを発見しました。日次GDPでも機械学習の手法を利用しようと思っているので、Bayesian Optimizationはかなり使える手法ではないかと思い、昨日徹夜で理解しました。その内容をここで実装しようとは思うのですが、Bayesian Optimizationではガウス回帰（Gaussian Pocess Regression,以下GPR）を使用しており、まずその実装を行おうと持ったのがこのエントリを書いた動機です。Bayesian Optimizationの実装はこのエントリの後にでも書こうかなと思っています。

GPRとは

GRPとは簡単に言ってしまえば「ベイズ推定を用いた非線形回帰手法の１種」です。モデル自体は線形ですが、カーネルトリックを用いて入力変数を無限個非線形変換したものを説明変数として推定できるところが特徴です（カーネルになにを選択するかによります）。GPRが想定しているのは、学習データとして入力データと教師データがそれぞれN個得られており、また入力データに関してはN+1個目のデータも得られている状況です。この状況から、N+1個目の教師データを予測します。教師データにはノイズが含まれており、以下のような確率モデルに従います。

t_{i} = y_{i} + \epsilon_{i}

ここで、t_{i}はi番目の観測可能な教師データ（スカラー）、y_{i}は観測できない出力データ（スカラー）、\epsilon_{i}は測定誤差で正規分布N(0,\beta^{-1})に従います。y_{i}は以下のような確率モデルに従います。

\displaystyle y_{i} = \textbf{w}^{T}\phi(x_{i})

ここで、x_{i}はi番目の入力データベクトル、\phi(・)は非線形関数、 \textbf{w}^{T}は各入力データに対する重み係数（回帰係数）ベクトルです。非線形関数としては、\phi(x_{i}) = (x_{1,i}, x_{1,i}^{2},...,x_{1,i}x_{2,i},...)を想定しています（x_{1,i}はi番目の入力データx_{i}の１番目の変数）。教師データの確率モデルから、i番目の出力データy_{i}が得られたうえでt_{i}が得られる条件付確率は、

p(t_{i}|y_{i}) = N(t_{i}|y_{i},\beta^{-1})

となります。\displaystyle \textbf{t} = (t_{1},...,t_{n})^{T}、\displaystyle \textbf{y} = (y_{1},...,y_{n})^{T}とすると、上式を拡張することで

\displaystyle p(\textbf{t}|\textbf{y}) = N(\textbf{t}|\textbf{y},\beta^{-1}\textbf{I}_{N})

と書けます。また、事前分布として\textbf{w}の期待値は0、分散は全て\alphaと仮定します。\displaystyle \textbf{y}はガウス過程に従うと仮定します。ガウス過程とは、\displaystyle \textbf{y}の同時分布が多変量ガウス分布に従うもののことです。コードで書くと以下のようになります。

# Define Kernel function
Kernel_Mat <- function(X,sigma,beta){
  N <- NROW(X)
  K <- matrix(0,N,N)
  for (i in 1:N) {
    for (k in 1:N) {
      if(i==k) kdelta = 1 else kdelta = 0
      K[i,k] <- K[k,i] <- exp(-t(X[i,]-X[k,])%*%(X[i,]-X[k,])/(2*sigma^2)) + beta^{-1}*kdelta
    }
  }
  return(K)
}

N <- 10 # max value of X
M <- 1000 # sample size
X <- matrix(seq(1,N,length=M),M,1) # create X
testK <- Kernel_Mat(X,0.5,1e+18) # calc kernel matrix

library(MASS)

P <- 6 # num of sample path
Y <- matrix(0,M,P) # define Y

for(i in 1:P){
  Y[,i] <- mvrnorm(n=1,rep(0,M),testK) # sample Y
}

# Plot
matplot(x=X,y=Y,type = "l",lwd = 2)

Kernel_Matについては後述しますが、\displaystyle \textbf{y}の各要素\displaystyle y_{i} = \textbf{w}^{T}\phi(x_{i})の間の共分散行列Kを入力xからカーネル法を用いて計算しています。そして、このKと平均0から、多変量正規乱数を6系列生成し、それをプロットしています。プロットしたものがこちらです。

f:id:osashimix:20190414112221p:plain

これらの系列は共分散行列から計算されるので、各要素の共分散が正に大きくなればなるほど同じ値をとりやすくなるようモデリングされていることになります。また、グラフを見ればわかるように非常になめらかなグラフが生成されており、かつ非常に柔軟な関数を表現できていることがわかります。コードでは計算コストの関係上、入力を0から10に限定して1000個の入力点をサンプルし、作図を行っていますが、原理的にはxは実数空間で定義されるものであるので、p(\textbf{y})は無限次元の多変量正規分布に従います。
以上のように、\displaystyle \textbf{y}はガウス過程に従うと仮定するので同時確率p(\textbf{y})は平均０、分散共分散行列がKの多変量正規分布N(\textbf{y}|0,K)に従います。ここで、Kの各要素K_{i,j}は、

K_{i,j} = cov[y_{i},y_{j}] = cov[\textbf{w}\phi(x_{i}),\textbf{w}\phi(x_{j})] \\ =\phi(x_{i})\phi(x_{j})cov[\textbf{w},\textbf{w}]=\phi(x_{i})\phi(x_{j})\alpha

です。ここで、\phi(x_{i})\phi(x_{j})\alphaは\phi(x_{i})の次元が大きくなればなるほど計算量が多くなります（つまり、非線形変換をかければかけるほど計算が終わらない）。しかし、カーネル関数k(x,x')を用いると、計算量は高々入力データx_{i},x_{j}のサンプルサイズの次元になるので、計算がしやすくなります。カーネル関数を用いてK_{i,j} = k(x_{i},x_{j})となります。カーネル関数としてはいくつか種類がありますが、以下のガウスカーネルがよく使用されます。

k(x,x') = a \exp(-b(x-x')^{2})

\displaystyle \textbf{y}の同時確率が定義できたので、\displaystyle \textbf{t}の同時確率を求めることができます。

\displaystyle p(\textbf{t}) = \int p(\textbf{t}|\textbf{y})p(\textbf{y}) d\textbf{y} \\ \displaystyle = \int N(\textbf{t}|\textbf{y},\beta^{-1}\textbf{I}_{N})N(\textbf{y}|0,K)d\textbf{y} \\ = N(\textbf{y}|0,\textbf{C}_{N})

ここで、\textbf{C}_{N} = K + \beta^{-1}\textbf{I}_{N}です。なお、最後の式展開は正規分布の再生性を利用しています（証明は正規分布の積率母関数から容易に導けます）。要は、両者は独立なので共分散は２つの分布の共分散の和となると言っているだけです。個人的には、p(\textbf{y})が先ほど説明したガウス過程の事前分布であり、p(\textbf{t}|\textbf{y})が尤度関数で、p(\textbf{t})は事後分布をというようなイメージです。事前分布p(\textbf{y})は制約の緩い分布でなめらかであることのみが唯一の制約です。
N個の観測可能な教師データ\textbf{t}とt_{N+1}の同時確率は、

p(\textbf{t},t_{N+1}) = N(\textbf{t},t_{N+1}|0,\textbf{C}_{N+1})

ここで、\textbf{C}_{N+1}は、

\textbf{C}_{N+1} = \left( \begin{array}{cccc} \textbf{C}_{N} & \textbf{k} \\ \textbf{k}^{T} & c \\ \end{array} \right)

です。ここで、\textbf{k} = (k(x_{1},x_{N+1}),...,k(x_{N},x_{N+1}))、c = k(x_{N+1},x_{N+1})です。\textbf{t}とt_{N+1}の同時分布から条件付分布p(t_{N+1}|\textbf{t})を求めることができます。

p(t_{N+1}|\textbf{t}) = N(t_{N+1}|\textbf{k}^{T}\textbf{C}_{N+1}^{-1}\textbf{t},c-\textbf{k}^{T}\textbf{C}_{N+1}^{-1}\textbf{k})

条件付分布の計算においては、条件付多変量正規分布の性質を利用しています（
条件付き多変量正規分布 - Qiita）。上式を見ればわかるように、条件付分布p(t_{N+1}|\textbf{t})はN+1個の入力データ、N個の教師データ、カーネル関数のパラメータa,bが既知であれば計算可能となっていますので、任意の点を入力データとして与えてやれば、元のData Generating Processを近似することが可能になります。GPRの良いところは上で定義した確率モデル\displaystyle y_{i} = \textbf{w}^{T}\phi(x_{i})を直接推定しなくても予測値が得られるところです。確率モデルには\phi(x_{i})があり、非線形変換により入力データを高次元ベクトルへ変換しています。よって、次元が高くなればなるほど\phi(x_{i})\phi(x_{j})\alphaの計算量は大きくなっていきますが、GPRではカーネルトリックを用いているので高々入力データベクトルのサンプルサイズの次元の計算量で事足りることになります。

GPRの実装

とりあえずここまでをRで実装してみましょう。PRMLのテストデータで実装しているものがあったので、それをベースにいじってみました。

library(ggplot2)
library(grid)

# 1.Gaussian Process Regression

# PRML's synthetic data set
curve_fitting <- data.frame(
  x=c(0.000000,0.111111,0.222222,0.333333,0.444444,0.555556,0.666667,0.777778,0.888889,1.000000),
  t=c(0.349486,0.830839,1.007332,0.971507,0.133066,0.166823,-0.848307,-0.445686,-0.563567,0.261502))

f <- function(beta, sigma, xmin, xmax, input, train) {
  kernel <- function(x1, x2) exp(-(x1-x2)^2/(2*sigma^2)); #ガウスカーネルを定義
  K <- outer(input, input, kernel); #グラム行列を計算
  C_N <- K + diag(length(input))/beta
  m <- function(x) (outer(x, input, kernel) %*% solve(C_N) %*% train) #条件付き分布の平均 
  m_sig <- function(x)(kernel(x,x) - diag(outer(x, input, kernel) %*% solve(C_N) %*% t(outer(x, input, kernel)))) #条件付き分布の分散
  x <- seq(xmin,xmax,length=100)
  output <- ggplot(data.frame(x1=x,m=m(x),sig1=m(x)+1.96*sqrt(m_sig(x)),sig2=m(x)-1.96*sqrt(m_sig(x)),
                              tx=input,ty=train),
                   aes(x=x1,y=m)) + 
    geom_line() +
    geom_ribbon(aes(ymin=sig1,ymax=sig2),alpha=0.2) +
    geom_point(aes(x=tx,y=ty))
  return(output)
}

grid.newpage() #空の画面を作る
pushViewport(viewport(layout=grid.layout(2, 2))) #画面を区切る（今回は2行2列の4分割）
print(f(100,0.1,0,2,curve_fitting$x,curve_fitting$t), vp=viewport(layout.pos.row=1, layout.pos.col=1)) #1行目の1
print(f(4,0.10,0,2,curve_fitting$x,curve_fitting$t), vp=viewport(layout.pos.row=1, layout.pos.col=2)) #1行目の2列
print(f(25,0.30,0,2,curve_fitting$x,curve_fitting$t), vp=viewport(layout.pos.row=2, layout.pos.col=1)  ) #2行目の1列
print(f(25,0.030,0,2,curve_fitting$x,curve_fitting$t), vp=viewport(layout.pos.row=2, layout.pos.col=2)  ) #2行目の2列

\beta,bにいくつかのパラメータを設定し(a=1)、グラフを書いてみました。

f:id:osashimix:20181209225109p:plain

\beta^{-1}は測定誤差を表しています。\betaが大きい（つまり、測定誤差が小さい）とすでに得られているデータとの誤差が少なくなるように予測値をはじき出すので、over fitting しやすくなります。上図の左上がそうなっています。左上は\beta=400で、現時点で得られているデータに過度にfitしていることがわかります。逆に\betaが小さいと教師データとの誤差を無視するように予測値をはじき出しますが、汎化性能は向上するかもしれません。右上の図がそれです。\beta=4で、得られているデータ点を平均はほとんど通っていません。bは現時点で得られているデータが周りに及ぼす影響の広さを表しています。bが小さいと、隣接する点が互いに強く影響を及ぼし合うため、精度は下がるが汎化性能は上がるかもしれません。逆に、bが大きいと、個々の点にのみフィットする不自然な結果になります。これは右下の図になります（b=\frac{1}{0.03},\beta=25）。御覧の通り、\betaが大きいのでoverfitting気味であり、なおかつbも大きいので個々の点のみにfitし、無茶苦茶なグラフになっています。左下のグラフが最もよさそうです。b=\frac{1}{0.3},\beta=2となっています。試しに、このグラフのx区間を[0,2]へ伸ばしてみましょう。すると、以下のようなグラフがかけます。

f:id:osashimix:20181209225312p:plain

これを見ればわかるように、左下以外のグラフはすぐに95%信頼区間のバンドが広がり、データ点がないところではまったく使い物にならないことがわかります。一方、左下のグラフは1.3~1.4ぐらいまではそこそこのバンドがかけており、我々が直感的に理解する関数とも整合的な点を平均値が通っているように思えます。また、観測可能なデータ点から離れすぎるとパラメータに何を与えようと平均０、分散１の正規分布になることもわかるがわかります。
さて、このようにパラメータの値に応じて、アウトサンプルの予測精度が異なることを示したわけですが、ここで問題となるのはこれらハイパーパラメータをどのようにして推計するかです。これは対数尤度関数\ln p(\textbf{t}|a,b)を最大にするハイパーパラメータを勾配法により求めます*1。p(\textbf{t}) = N(\textbf{y}|0,\textbf{C}_{N})なので、対数尤度関数は

\displaystyle \ln p(\textbf{t}|a,b,\beta) = -\frac{1}{2}\ln|\textbf{C}_{N}| - \frac{N}{2}\ln(2\pi) - \frac{1}{2}\textbf{t}^{T}\textbf{C}_{N}^{-1}\textbf{k}

となります。あとは、これをパラメータで微分し、得られた連立方程式を解くことで最尤推定量が得られます。ではまず導関数を導出してみます。

\displaystyle \frac{\partial}{\partial \theta_{i}} \ln p(\textbf{t}|\theta) = -\frac{1}{2}Tr(\textbf{C}_{N}^{-1}\frac{\partial \textbf{C}_{N}}{\partial \theta_{i}}) + \frac{1}{2}\textbf{t}^{T}\textbf{C}_{N}^{-1} \frac{\partial\textbf{C}_{N}}{\partial\theta_{i}}\textbf{C}_{N}^{-1}\textbf{t}

ここで、\thetaはパラメータセットで、\theta_{i}はi番目のパラメータを表しています。この導関数が理解できない方はPRMLの補論にある(C.21)式と(C.22)式をご覧になると良いと思います。今回はガウスカーネルを用いているため、

\displaystyle \frac{\partial k(x,x')}{\partial a} = \exp(-b(x-x')^{2}) \\ \displaystyle \frac{\partial k(x,x')}{\partial b} = -a(x-x')^{2}\exp(-b(x-x')^{2})

を上式に代入すれば良いだけです。ただ、今回は勾配法により最適なパラメータを求めます。以下、実装のコードです（かなり迷走しています）。


g <- function(xmin, xmax, input, train){
  # 初期値
  beta = 100
  b = 1
  a = 1
  learning_rate = 0.1
  if (class(input) == "numeric"){
    N <- length(input)
  } else
  {
    N <- NROW(input)
  }
  kernel <- function(x1, x2) a*exp(-0.5*b*(x1-x2)^2); #ガウスカーネルを定義
  derivative_a <- function(x1,x2) exp(-0.5*b*(x1-x2)^2)
  derivative_b <- function(x1,x2) -0.5*a*(x1-x2)^2*exp(-0.5*b*(x1-x2)^2)
  dloglik_a <- function(C_N,y,x1,x2) {
    -sum(diag(solve(C_N)%*%outer(input, input, derivative_a)))+t(y)%*%solve(C_N)%*%outer(input, input, derivative_a)%*%solve(C_N)%*%y 
  }
  dloglik_b <- function(C_N,y,x1,x2) {
    -sum(diag(solve(C_N)%*%outer(input, input, derivative_b)))+t(y)%*%solve(C_N)%*%outer(input, input, derivative_b)%*%solve(C_N)%*%y 
  }
  # 対数尤度関数
  likelihood <- function(b,a,x,y){
    kernel <- function(x1, x2) a*exp(-0.5*b*(x1-x2)^2)
    K <- outer(x, x, kernel)
    C_N <- K + diag(N)/beta
    l <- -1/2*log(det(C_N)) - N/2*(2*pi) - 1/2*t(y)%*%solve(C_N)%*%y
    return(l)
  }
  K <- outer(input, input, kernel) 
  C_N <- K + diag(N)/beta
  for (i in 1:itermax){
    kernel <- function(x1, x2) a*exp(-b*(x1-x2)^2)
    derivative_b <- function(x1,x2) -0.5*a*(x1-x2)^2*exp(-0.5*b*(x1-x2)^2)
    dloglik_b <- function(C_N,y,x1,x2) {
      -sum(diag(solve(C_N)%*%outer(input, input, derivative_b)))+t(y)%*%solve(C_N)%*%outer(input, input, derivative_b)%*%solve(C_N)%*%y 
    }
    K <- outer(input, input, kernel) #グラム行列を計算
    C_N <- K + diag(N)/beta
    l <- 0
    if(abs(l-likelihood(b,a,input,train))<0.0001&i>2){
      break
    }else{
      a <- as.numeric(a + learning_rate*dloglik_a(C_N,train,input,input))
      b <- as.numeric(b + learning_rate*dloglik_b(C_N,train,input,input))
    }
    l <- likelihood(b,a,input,train)
  }
  K <- outer(input, input, kernel)
  C_N <- K + diag(length(input))/beta
  m <- function(x) (outer(x, input, kernel) %*% solve(C_N) %*% train)  
  m_sig <- function(x)(kernel(x,x) - diag(outer(x, input, kernel) %*% solve(C_N) %*% t(outer(x, input, kernel))))
  x <- seq(xmin,xmax,length=100)
  output <- ggplot(data.frame(x1=x,m=m(x),sig1=m(x)+1.96*sqrt(m_sig(x)),sig2=m(x)-1.96*sqrt(m_sig(x)),
                              tx=input,ty=train),
                   aes(x=x1,y=m)) + 
    geom_line() +
    geom_ribbon(aes(ymin=sig1,ymax=sig2),alpha=0.2) +
    geom_point(aes(x=tx,y=ty))
  return(output)
}

print(g(0,1,curve_fitting$x,curve_fitting$t), vp=viewport(layout.pos.row=1, layout.pos.col=1))

求められたパラメータを用いて推定した結果が以下です。

f:id:osashimix:20181209225503p:plain

たしかに、良さそうな感じがします（笑）
とりあえず、今日はここまで。

*1:\betaは少しタイプが異なるようで、発展的な議論では他のチューニング方法をとる模様。まだ、そのレベルにはいけていないのでここではカリブレートすることにします。

【日次GDP】BVARについて

　おはこんばんにちは。日次GDP推計を休日に進めているのですが、今日は少し勉強編でBVARについての記事を書きたいと思います。このBVARはFRBアトランタ連銀のGDPNowでも使用されていることから、日次GDP推計との親和性も高いと思われます。そもそも、時系列でアウトサンプルの予測精度を上げたいということになると真っ先に思いつくのがBVARです。Doan, Litterman and Sims(1984)で提案されたこのモデルは予測精度が良いので、非常に有効な手段になると思われます。BVARはBayesian Vector Autoregressionの略で、ベクトル自己回帰モデル（VAR）の派生版です。「VAR」とネットで調べるとまずValue at Risk（VaR）が出てくると思いますが、それとは違います。よく見るとaが小文字になっていることに気づくかと思います。
　さて、BVARの説明をこれから行おうとするのですが、その前にまず基本的なVARの説明からしたいと思います。ただし、歴史的な背景（大型マクロ計量モデルからの経緯など）には触れません。あくまで、BVARを説明するうえで必要な知識について触れたいと思います。

Unrestricted VARについて

　まず、注意点を一点。この投稿では、もっとも基本的なVARのことをUnrestricted VAR（UVAR）と呼ぶことにします。UVARはSims(1980)の論文が有名です*1。このモデルには、理論的な基礎づけは原則ありません。あくまで実証的なモデルです。UVARは一般系は以下のような形をしています。

Y_{t} = A_{0} + A_{1}Y_{t-1} + ... + A_{K}Y_{t-K} + U_{t}, U_{t} ～ N(0,\Omega) \\ Y_{t} = \left( \begin{array}{cccc} y_{1,t} \\ y_{2,t} \\ \vdots \\ y_{J,t} \\ \end{array} \right), A_{0} = \left( \begin{array}{cccc} a_{10} \\ a_{20} \\ \vdots \\ a_{J0} \\ \end{array} \right), A_{k} = \left( \begin{array}{cccc} a_{11,k} & a_{12,k} & \ldots & a_{1J,k} \\ a_{21,k} & a_{22,k} & \ldots & a_{2J,k} \\ \vdots & \vdots & \ddots & \vdots \\ a_{J1,k} & a_{J2,k} & \ldots & a_{JJ,k} \end{array} \right), U_{t} = \left( \begin{array}{cccc} u_{1,t} \\ u_{2,t} \\ \vdots \\ u_{J,t} \\ \end{array} \right)

ここで、tは時点、Jは変数の数、Kはラグ数を表しています。上式を見ると、UVARは自己回帰＋他変数のラグでt期の変数y_{j,t}を説明しようとするモデルであると言えます。しばしば、経済の実証分析で使用され、インサンプルの当てはまりが良いことも知られています（GDP、消費、投資、金利、マネーサプライの５変数VARで金融政策の波及経路を分析したり･･･）。推定するパラメータの個数は、回帰式1本だけでJK+1個（定数項込み）の係数を含むので、J本になればJ(JK+1)個になります。また、\OmegaがJ(J+1)/2個のパラメータを持っているので、合計J(JK+1)+J(J+1)/2個のパラメータを推定することになり、かなりパラメータ数が多い印象です（これは後々重要になってきます）。具体的な推計方法ですが、UVARは同時方程式体系ではないのでそこまで面倒ではありません。UVAR自体はSeemingly Unrestricted Regression Equation（SUR）の一種でそれぞれの方程式は誤差項の相関を通じて関係してはいますが（\Omegaの部分）、全ての回帰式が同じ説明変数を持つため、各方程式を最小二乗法（OLS）によって推定するだけで良いことが知られています。
　この事実を説明してみましょう（BVARが気になる方は読み飛ばしてもらって構いません）。説明のために今、UVARをSURの一般系に書き直します。上式はt期のVAR(K)システムですが、UVARを推定する際はこれらJ本の方程式がサンプル数Tセット分存在するので、実際のシステム体系は以下のようになります。

\left( \begin{array}{cccc} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{J} \\ \end{array} \right) = \left( \begin{array}{cccc} X_{1} & 0 & \ldots & 0 \\ 0 & X_{2} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & X_{J} \end{array} \right) \left( \begin{array}{cccc} A_{1} \\ A_{2} \\ \vdots \\ A_{J} \\ \end{array} \right) + \left( \begin{array}{cccc} U_{1} \\ U_{2} \\ \vdots \\ U_{J} \\ \end{array} \right) = \overline{X}A + U (1式)

ここで、

Y_{j} = \left( \begin{array}{cccc} y_{t,j} \\ y_{t+1,j} \\ \vdots \\ y_{T,j} \\ \end{array} \right) , X_{j} = X = \left( \begin{array}{cccc} 1 & y_{t-1,1} & \ldots & y_{t-K,1} & \ldots & y_{t-K,J} \\ 1 & y_{t,1} & \ldots & y_{t-K+1,1} & \ldots & y_{t-K+1,J} \\ \vdots & \vdots & \ldots & \ldots & \ddots & \vdots \\ 1 & y_{T-1,1} & \ldots & y_{T-K,1} & \ldots & y_{T-K,J} \\ \end{array} \right), A_{j} = \left( \begin{array}{cccc} a_{00,j} \\ a_{11,j} \\ \vdots \\ a_{JK,j} \\ \end{array} \right)

です。上式とは違い、変数順で並べられていることに注意してください（つまり、各方程式を並べる優先順位は１番目にj、２番目にtとなっている）。また、X_{j}が全ての変数jについて等しいことに注目してください（jに依存していません、VARなので当たり前ですが）。これが後々非常に重要になってきます。Uの分散共分散行列は

E[UU'|X_{1}, X_{2},..,X_{J}] = \Omega = \left( \begin{array}{cccc} \sigma_{11}I & \sigma_{12}I & \ldots & \sigma_{1J}I \\ \sigma_{21}I & \sigma_{22}I & \ldots & \sigma_{2J}I \\ \vdots & \vdots & \ddots & \vdots \\ \sigma_{J1}I & \sigma_{J2}I & \ldots & \sigma_{JJ}I \\ \end{array} \right)

となっており、それぞれの変数は誤差項の相関を通じて関係しています（ただし、同じ変数内の異なる時点間の相関はないと仮定します）。このような場合、一般化最小二乗法（GLS）を用いて推計を行うことになりますが、これら方程式体系において説明変数が同じであるならば、GLS推定量とOLS推定量は同値になります。それを確かめてみましょう。上述した方程式体系(1)のGLS推定量は以下になります（GLS推定に関してはこちらを参照）。

A_{GLS} = (\overline{X}'\Omega^{-1}\overline{X})^{-1}\overline{X}'\Omega^{-1}Y = (\overline{X}'(\Sigma^{-1}\otimes I)\overline{X})^{-1}\overline{X}'(\Sigma^{-1}\otimes I)Y

ここで、\Sigmaは誤差項の分散共分散行列のうち、スカラーである分散、共分散を取り出した行列です。先ほど確認したように、X_{1}=X_{2}=...=X_{J}=Xなので\overline{X}=I \otimes Xであり、その転置も\overline{X}'=I \otimes Xとなります。よって、クロネッカー積の混合積の性質を用いると、

A_{GLS} = [(I \otimes X')(\Sigma^{-1}\otimes I)(I \otimes X)]^{-1}(I \otimes X')(\Sigma^{-1}\otimes I)Y \\ = [(\Sigma^{-1}\otimes X')(I \otimes X)]^{-1}(\Sigma^{-1}\otimes X')y \\ = (\Sigma^{-1}\otimes(X'X))^{-1}(\Sigma^{-1}\otimes X')y \\ = (I \otimes (X'X)^{-1}X')y \\ = (\overline{X}'\overline{X})^{-1}\overline{X}'Y \\ = \left( \begin{array}{cccc} (X'X)^{-1}X' & 0 & \ldots & 0 \\ 0 & (X'X)^{-1}X' & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & (X'X)^{-1}X' \end{array} \right) \left( \begin{array}{cccc} Y_{1} \\ Y_{2} \\ \vdots \\ Y_{J} \\ \end{array} \right)\\ = \left( \begin{array}{cccc} (X'X)^{-1}X'Y_{1} \\ (X'X)^{-1}X'Y_{2} \\ \vdots \\ (X'X)^{-1}X'Y_{J} \\ \end{array} \right) = \left( \begin{array}{cccc} A_{1,OLS} \\ A_{2,OLS} \\ \vdots \\ A_{J,OLS} \\ \end{array} \right)

となり、各経済変数の方程式を別個にOLS推計していけばよいことがわかります。
　OLS推定に際し、VARの次数Kの選択を選択する必要がありますが、次数KはAIC（BIC）を評価軸に探索的に決定します。つまり、いろいろな値をKに設定し、OLS推計を行い、計算されたVAR(K)のAIC(BIC)のうちで最も値が大きいモデルの次数を真のモデルの次数Kとして採用するということです。RにもVARselect()という関数があり、引数にラグの探索最大数とデータを渡すことで最適な次数を計算してくれます（便利）。
　このようにUVARはOLS推計で各変数間の相互依存関係をデータから推計できる手軽な手法です。私が知っている分野ですと財政政策乗数の推計に使用されていました。GDP、消費、投資、政府支出の４変数でVARを推定し、推定したVARでインパルス応答を見ることで１単位の財政支出の増加がGDP等に与える影響を定量的にシミュレートすることができたりします（指導教官が論文を書いてました）。そもそも私の専門のDSGEも誘導系に書き直せばVAR形式になり、インパルス応答などは基本的に一緒です。また、経済変数は慣性が強いので（特に我が国の場合）、インサンプルのモデルの当てはまりもいいです。ただし、あくまでインサンプルです。アウトサンプルの当てはまりはそれほど良い印象はありません。なぜなら、推定パラメータが多すぎるからです。UVARの予測に関する問題点はover-parametrizationです。例えば、先ほどの４変数UVARでラグが６期だったとすると、推定すべきパラメータは３１個になります。よって、データ数にもよりますが、パラメータ数がデータ数に近づくとインサンプルの補間に近づき、過学習を引き起こす危険性があります。日次GDP推計は大量の変数を使用するのでこの問題は非常に致命的になります。BVARはこの問題を解決することに主眼を置いています。

BVARについて

　UVARの問題点はover-parametrizationであると述べました。BVARはこの問題を防ぐために不必要な説明変数（のパラメータ）をそぎ落とそうとします。ただ、不要なパラメータを推定する前に０と仮置き（カリブレート）するのではなく、１階の自己に関わるパラメータは１周り、その他変数のパラメータは０周りに正規分布するという形の制約を与えます。このモデルの最大の仮定は「各経済変数は多かれ少なかれドリフト付き１階のランダムウォークに従う」というものであり、上述したような事前分布を先験的に与えた上で推定を行うのです。砕けた言い方をすると、BVARの考え方は「経済変数の挙動は基本はランダムウォークだけど他変数のラグに予測力向上に資するものがあればそれも取り入れるよ」というものなんです。さて、前置きが長くなりましたが、具体的な説明に移りたいと思います。

具体的な推定方法（カルマンフィルタ）

　上述した事前分布に加えて、BVARがUVARと異なる点はパラメータがtime-varyingであるということです。なんとなく、パラメータがずっと固定よりもサンプルが増えるたびにその値が更新されるほうが予測精度が上がりそうですよね（笑）。推定手法としてはUVARの時のようにOLSをそれぞれにかけることはせず、カルマンフィルタと呼ばれるアルゴリズムを用いて推定を行います。BVARは以下のような状態空間モデルとして定義されます（各ベクトル、行列の次元はUVAR時と同じです）。

Y_{t} = X_{t}B_{t} + u_{t} \\ B_{t} = \Phi B_{t-1} + \epsilon_{t} \\ B_{t} = \left( \begin{array}{cccc} \beta_{00,t} \\ \beta_{11,t} \\ \vdots \\ \beta_{JK,t} \\ \end{array} \right), \Phi = \left( \begin{array}{cccc} \phi_{00} & 0 & \ldots & 0 \\ 0 & \phi_{11} & \ldots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \ldots & \phi_{JK} \end{array} \right), u_{t} = \left( \begin{array}{cccc} u_{1,t} \\ u_{2,t} \\ \vdots \\ u_{J,t} \\ \end{array} \right), \epsilon_{t} = \left( \begin{array}{cccc} \epsilon_{00,t} \\ \epsilon_{11,t} \\ \vdots \\ \epsilon_{JK,t} \\ \end{array} \right)

状態空間モデルは観測可能なデータ（ex.経済統計）を用いて、観測不可能なデータ（ex.リスクプレミアムや限界消費性向等）を推定します。観測可能なデータと不可能なデータを関連付ける方程式を観測方程式、観測不可能なデータの挙動をモデル化した方程式を遷移方程式と呼びます。ここでは、1本目が観測方程式、2本目が遷移方程式となります。御覧の通り、観測方程式は通常のVARの形をしている一方、遷移方程式はAR(1)となっており、これによってパラメータB_{t}は過去の値を引きずりながら\epsilon_{t}によって確率的に変動します。\Phiは自己回帰係数です。誤差項u_{t}と\epsilon_{t}は平均０の正規分布に従い、その分散は

Var(u_{t}) = \sigma_{u}^{2} \\ Var(\epsilon_{t}) = \sigma_{\epsilon}^{2}R

で与えられます。ここで、\Phi,R,\sigma_{u}^{2},\sigma_{\epsilon}^{2}は既知であるとします。今、t-1期までのデータが入手可能であるとすると、そのデータをカルマンフィルタアルゴリズムで推定したB_{t-1|t-1}とその分散共分散行列P_{t-1|t-1}を用いて、t期の予想値を以下のように計算します。

B_{t|t-1} = \Phi B_{t-1|t-1} \\ P_{t|t-1} = \Phi P_{t|t-1} \Phi' + \sigma_{\epsilon}^{2}R

観測可能な変数の予測値はこの値を用いて計算します。

\hat{Y_{t}} = X_{t} B_{t|t-1}

次にt期の観測値が得られると次の更新方程式を用いてB_{t|t}, P_{t|t}を計算します。

B_{t|t} = B_{t|t-1} + P_{t|t-1}X_{t}'(X_{t}P_{t|t-1}X_{t}' + \sigma_{u}^{2})^{-1}(Y_{t}-X_{t}B_{t|t-1}) \\ P_{t|t} = P_{t|t-1} + P_{t|t-1}X_{t}'(X_{t}P_{t|t-1}X_{t}' + \sigma_{u}^{2})^{-1}X_{t}P_{t|t-1}

\sigma_{\epsilon}^{2}R = 0かつ\Phi = Iの場合は逐次最小二乗法に一致します。要は入手できるサンプル増えるたびにOLSをやり直していくことと同値だということです。こうして推計を行うのがBVARなのですが、カルマンフィルタは漸化式なので初期値B_{0|0}, P_{0|0}を決めてやる必要があります。BVARの２つ目の特徴は初期値の計算に混合推定法を用いているところであり、ここに前述した事前分布が関係してきます。

カルマンフィルタの初期値をどのようにきめるか

初期値B_{0|0}, P_{0|0}をどうやって計算するのかを考えた際にすぐ思いつく方法としては、カルマンフィルタのスタート地点tの前に、初期値推計期間をある程度用意し、Y = XB + \epsilonでB_{0|0}, P_{0|0}を推定する方法があります。つまり、観測方程式をGLS推計し、そのパラメータを初期値とする方法です。その際のGLS推定量は

\hat{B} = (X'V^{-1}X)^{-1}X'V^{-1}Y

です。これでもいいんですが、これではただ時変パラメータを推計しているだけで先ほど述べたover-parametrizationの問題にはアプローチできていません。そこで、ここではパラメータBに対してなにか先験的な情報が得られているとしましょう。つまり、先述した「経済変数の挙動は基本はランダムウォークだけど他変数のラグに予測力向上に資するものがあればそれも取り入れるよ」という予想です。これを定式化してみましょう。つまり、パラメータBに対して以下の制約式を課します。

r = RB + \nu

ここで、 E(\nu) = 0,Var(\nu) = V_{0}です。また、rはRBの予想値であり、V_{0}はその予想値の周りでのばらつきを表しています。取っ付きにくいかもしれませんが、rは１階自己回帰係数に関わる部分は1、それ以外は0となるベクトルで、Rは単位行列Iだと思ってもらえばいいです。つまり、

\left( \begin{array}{cccc} 0 \\ 1 \\ 0 \\ \vdots \\ 1 \\ \vdots \\ 0 \\ \end{array} \right) = \left( \begin{array}{cccc} 　 \beta_{0,1}^{1} \\ \beta_{1,1}^{1} \\ \beta_{2,1}^{1} \\ \vdots \\ \beta_{j,1}^{j} \\ \vdots \\ \beta_{J,K}^{J} \\ \end{array} \right) + \left( \begin{array}{cccc} \nu_{0,1}^{1} \\ \nu_{1,1}^{1} \\ \nu_{2,1}^{1} \\ \vdots \\ \nu_{j,1}^{j} \\ \vdots \\ \nu_{J,K}^{J} \\ \end{array} \right)

みたいな感じです。ここで\beta_{j,k}^{i}はi番目の方程式のj番目の変数のk次ラグにかかるパラメータを表しています。混合推定では、正規分布に従う観測値とこの事前分布が独立であるという仮定の下で観測方程式Y = XB + \epsilonと r = RB + \nuを以下のように組み合わせます。

\left( \begin{array}{cccc} Y \\ r \end{array} \right) = \left( \begin{array}{cccc} X \\ R \end{array} \right)B + \left( \begin{array}{cccc} \epsilon \\ \nu \end{array} \right)

ここで、

E\left( \begin{array}{cccc} \epsilon \\ \nu \end{array} \right) = 0 \\ Var\left( \begin{array}{cccc} \epsilon \\ \nu \end{array} \right) = \left( \begin{array}{cccc} \sigma^{2}V & 0 \\ 0 & V_{0} \\ \end{array} \right)

そして、このシステム体系をGLSで推計するのです。こうすることで、事前分布を考慮した初期値の推定を行うことができます。GLS推定量は以下のようになります。

\displaystyle \hat{B}_{M} = (\frac{1}{\sigma^{2}}X'V^{-1}X + R'V_{0}^{-1}R)^{-1}(\frac{1}{\sigma^{2}}X'V^{-1}y + R'V_{0}^{-1}r)

ご覧になればわかるように、GLS推定量は上記2本の連立方程式(実際には行列なので何本もありますが)それぞれのGLS推定量を按分したような推定量になります。ここで、\sigma^{2}は既知ではないので、いったんOLSで推計しその推定量を用います。問題はV_{0}の置き方です。V_{0}の各要素を小さくとれば、事前分布に整合的な推定量が得られます（つまり、ランダムウォーク）。逆に、大きくとれば通常のGLS推定量に近づいていきます。Doan, Litternam and Sims (1984)では以下のように分散を置いています。

\displaystyle Var(\beta_{j,k}^{j}) = \frac{\pi_{5}・\pi_{1}}{k・exp(\pi_{4}w_{i}^{i})} \\ \displaystyle Var(\beta_{j,k}^{i}) = \frac{\pi_{5}・\pi_{2}・\sigma_{i}^{2}}{k・exp(\pi_{4}w_{j}^{i})・\sigma_{j}^{2}} \\ Var(c^{i}) = \pi_{5}・\pi_{3}・\sigma_{i}^{2}

ここで、\beta_{j,k}^{j}はi番目の方程式の自己回帰パラメータ、\beta_{j,k}^{i}はi番目方程式の他変数ラグ項にかかるパラメータ、c^{i}は定数項です。そして、\pi_{1},\pi_{2},\pi_{3},\pi_{4},\pi_{5}はハイパーパラメータと呼ばれるもので、カルマンフィルタにかけるパラメータの初期値の事前分布の分布の広がりを決定するパラメータとなっています。これらは初期値の推定を行う前に値を指定する必要があります。各ハイパーパラメータの具体的な特徴は以下の通りです。\pi_{1}は\beta_{j,k}^{j}の分散にのみ出現することから自己回帰係数に影響を与えるパラメータとなっています。具体的には、\pi_{1}が大きくなればなるほど自己回帰係数は事前分布から大きく離れた辺りを取りうることになります。\pi_{2}は\beta_{j,k}^{i}の分散にのみ出現することから他変数のラグ項に影響を与えるパラメータとなっています。こちらも値が大きくなればなるほど係数は事前分布から大きく離れた辺りを取りうることになります。\pi_{3}は定数項の事前分布に影響を与えるパラメータでこちらも考え方は同じです。\pi_{4}はラグ項の分散(つまり定数項以外)に影響を与えるパラメータで、値が大きくなるにつれ、初期値は事前分布に近づいていきます。最後に\pi_{5}ですが、こちらは全体にかかるパラメータで、値が大きくなるにつれ、初期値は事前分布から遠ざかります。
　上式には、ハイパーパラメータ以外にもパラメータや変数が存在します。\sigma_{i}, \sigma_{j}はy_{j,t}, y_{i,t}をそれぞれAR(m)でフィッティングをかけた時の残差の標準偏差の推定値です。変数間のスケーリングの違いを考慮するために、\sigma_{i}を\sigma_{j}で割ったものを使用しています。本来ならば、VARの残差の標準偏差を使用すべきなのですが、推定する前にわかるわけもないので、それぞれAR(m)で推定をかけ、その標準偏差を使用しています*2。w_{j}^{i}は完全に恣意的なパラメータで、DLSではrelative weightsと呼ばれているものです。i番目の方程式のj番目の変数のラグ項にかかるパラメータが０であるかどうかについて、分析者の先験情報を反映するためのパラメータです。分散の式を見ればわかるように、relative weightが大きくなれば分散は小さくなり、推定値は事前分布に近づいていきます。DLSでは、ほとんどの変数はw_{i}^{i}=0,w_{j}^{i}=1でよいと主張されています。つまり、自己ラグにかかる事前分布の分散に関しては確信をもってランダムウォークであるといえる一方、他変数ラグについては予測力向上に役立つもののあることを考え、値を１と置いているのです。一方、為替レートや株価はランダムウォーク色が強いということから大きい値を使用しています。最後に、Var(\beta_{j,k}^{j})とVar(\beta_{j,k}^{i})には分母にkがついています。つまり、ラグ次数kが大きくなればなるほど、その係数は０に近づいていくことを先験的情報として仮定していることになります*3。
　これらがいわゆるMinnesota Priorの正体です*4。初期値が事前分布に近づけばBVARはランダムウォークに近づきますし、離れるとUVARに近づきます。現実はその間となるのですが、なにを評価尺度としてハイパーパラメータの値を決めるかというと、それは当てはまりの良さということになります。

ハイパーパラメータの決定方法とその評価尺度

当てはまりの良さと言ってもいろいろありますが、DLSはその時点で観測可能なデータから予測できるk期先の予測値の当てはまりの良さを基準としています。DLSでは以下の予測誤差ベクトル\hat{\epsilon}_{t+k|t}のクロス積和を最小化することを目的関数として、ハイパーパラメータのチューニングを行っています。

\hat{\epsilon}_{t+k|t} = \hat{Y}_{t+k|t}-Y_{t+k}

ここで、\hat{Y}_{t+k|t}はカルマンフィルタによるk期先の予測値です（kをいくつ先にすれば良いかは不明）。このクロス積は\hat{\epsilon}_{t+k|t}\hat{\epsilon}'_{t+k|t}であり、これをフィルタリングをかけるt=1期からサンプル期間であるt=T期まで計算していくので、最終的にはT個の予測誤差ベクトルを得ることになり、以下のようなこれらの総和を最小化します。

\displaystyle \sum_{t=1}^{T-k}\hat{\epsilon}_{t+k|t}\hat{\epsilon}'_{t+k|t}

より厳密にはこのクロス積和の対数値を最小化するハイパーパラメータの値をグリッドサーチやランダムサーチで探索していくことになります*5。
とまあ、BVARの推定方法はこんな感じです。他のVARと違い、恣意的であり、また推定方法が機械学習に近い点が特徴ではないかと思います。そもそも、BVARは予測に特化したVARですから、他のVARとは別物と考える方が良いかもです。

*1:Sims, Christopher A, 1980. "Macroeconomics and Reality," Econometrica, Econometric Society, vol. 48(1), pages 1-48, January.

*2:ランダムウォークが先験情報なので整合性は取れているような気がします

*3:このおかげでVARの次数をこちらで指定する必要がなくなります。適当に大きい次数を指定しておけば、必要のない次数の大きいパラメータに関しては事前と値が０になるので。

*4:実はこれに加えて自己回帰パラメータの総和が１、他変数のラグ項にかかるパラメータの総和が０となる制約を課すのですが、話が複雑になりすぎるので今回は割愛しました

*5:ここは機械学習等で用いられているベイズ最適化を利用するとより高速に収束させることが可能かもです。

【備忘】IFrameの中にある要素を取得するVBAコード

昨日、投降したVBAでネット上のファイルをダウンロードするマクロですが、どうやらご希望に添えるものではなかったようです。なんでも、IFrameがDOMにあったために、要素にたどり着けないんだとか。調べてみると、IFrameがあるDOMは一度IFrameのsrcを取得し、そこにNavigateしてから再度要素を取得しなければ取れないようです。 今回はアマゾンにあるフィギュアの画像を取るコードを書いていきたいと思います。

f:id:osashimix:20181029230214p:plain

御覧の通り、このページにはIFrameが入っています。今回はここから澪ちゃんのかわいい画像を保存するVBAを書きたいと思います（ファイルのダウンロードはないので）。

' Windows APIを呼び出すためのおまじない
Declare Function URLDownloadToFile Lib "urlmon" Alias _
    "URLDownloadToFileA" (ByVal pCaller As Long, _
    ByVal szURL As String, _
    ByVal szFileName As String, _
    ByVal dwReserved As Long, _
    ByVal lpfnCB As Long) As Long

Sub IFrame()

 Dim objIE As New InternetExplorer
 Dim URL As String, productTitle As String
 Dim objFrame As Object
 Dim result As Long
 
' おなじみの処理
 objIE.Visible = True
 URL = "https://www.amazon.co.jp/????????-?H?R?Y-1-7?X?P?[??-PVC?h?????????i/dp/B0041N46YS/ref=pd_sbs_0_5?_encoding=UTF8&pd_rd_i=B0041N46YS&pd_rd_r=a406524c-db7e-11e8-839d-5bb4d62fdf30&pd_rd_w=uhimH&pd_rd_wg=aIcmG&pf_rd_i=desktop-dp-sims&pf_rd_m=AN1VRQENFRJN5&pf_rd_p=cda7018a-662b-401f-9c16-bd4ec317039e&pf_rd_r=CMY0BXR864H44YSETHH0&pf_rd_s=desktop-dp-sims&pf_rd_t=40701&psc=1&refRID=CMY0BXR864H44YSETHH0"
 objIE.Navigate URL
 Do Until objIE.ReadyState = READYSTATE_COMPLETE
     DoEvents
 Loop

' IFrameタグの一番目を抽出し、そのソースコードへ移動（画面上に変化はなし） 
 Set objFrame = objIE.document.getElementsByTagName("iframe")(0)
 objIE.Navigate objFrame.getAttribute("src")
 
' うまく取れているか試すために商品名を抽出
 productTitle = objIE.document.getElementById("productTitle").innerText
 Debug.Print productTitle

' 画像のリンクを保存
 link = objIE.document.getElementById("landingImage").src
 
' ファイル名を取得
Filename = Mid(link, InStrRev(link, "/") + 1)
saveName = "C:\Users\aashi\Pictures" & "\" & Filename

' ダウンロードを実行
result = URLDownloadToFile(0, link, saveName, 0, 0)

End Sub

とれました。

f:id:osashimix:20181029231152p:plain

ここまで書いて判明したことですが、別にこのページに関してはIFrameのsrcを読み込まなくてもDLできました。けど、たぶんIFrameの中に組み込まれている要素もとれるはず（サンプルとなるページが見当たりませんでした）。 調べているとこんなページも見つけました。HTMLIFrameという変数の型があるらしく、そのプロパティやメソッドを使っているらしいです。具体的にどんなものかはまだ調べられていませんが、これを駆使するのも一つの方法かもしれません。